Data-Adaptive Symmetric CUSUM for Sequential Change Detection
- PMID: 40241737
- PMCID: PMC12002415
- DOI: 10.1080/07474946.2023.2272908
Data-Adaptive Symmetric CUSUM for Sequential Change Detection
Abstract
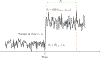
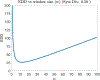
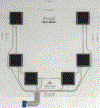
Detecting change points sequentially in a streaming setting, especially when both the mean and the variance of the signal can change, is often a challenging task. A key difficulty in this context often involves setting an appropriate detection threshold, which for many standard change statistics may need to be tuned depending on the pre-change and post-change distributions. This presents a challenge in a sequential change detection setting when a signal switches between multiple distributions. Unfortunately, change point detection schemes that use the log-likelihood ratio, such as CUSUM and GLR, are quick to react to changes but are not symmetric when both the mean and the variance of the signal change. This makes it difficult to set a single threshold to detect multiple change points sequentially in a streaming setting. We propose a modified version of CUSUM that we call Data-Adaptive Symmetric CUSUM (DAS-CUSUM). The DAS-CUSUM procedure is symmetric for changes between distributions, making it suitable to set a single threshold to detect multiple change points sequentially in a streaming setting. We provide results that relate the expected detection delay and average run length for our proposed procedure when both pre-change and post-change distributions are normally distributed. Experiments on simulated and real world data show the utility of DAS-CUSUM.
Keywords: Changes in mean and variance; False-alarm control; change-point detection.
Figures
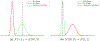

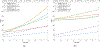

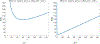
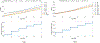
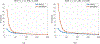
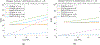
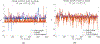
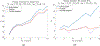
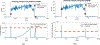
Similar articles
-
Single and Multiple Change Point Detection in Spike Trains: Comparison of Different CUSUM Methods.Front Syst Neurosci. 2016 Jun 22;10:51. doi: 10.3389/fnsys.2016.00051. eCollection 2016. Front Syst Neurosci. 2016. PMID: 27445714 Free PMC article.
-
Enhanced cumulative sum charts for monitoring process dispersion.PLoS One. 2015 Apr 22;10(4):e0124520. doi: 10.1371/journal.pone.0124520. eCollection 2015. PLoS One. 2015. PMID: 25901356 Free PMC article.
-
Monitoring surgical and medical outcomes: the Bernoulli cumulative SUM chart. A novel application to assess clinical interventions.Postgrad Med J. 2005 Oct;81(960):647-52. doi: 10.1136/pgmj.2004.030619. Postgrad Med J. 2005. PMID: 16210461 Free PMC article.
-
A Comprehensive Review and Comparison of CUSUM and Change-Point-Analysis Methods to Detect Test Speededness.Multivariate Behav Res. 2022 Jan-Feb;57(1):112-133. doi: 10.1080/00273171.2020.1809981. Epub 2020 Sep 2. Multivariate Behav Res. 2022. PMID: 32877253 Review.
-
Monitoring surgical quality: the cumulative sum (CUSUM) approach.Mediastinum. 2020 Mar 25;4:4. doi: 10.21037/med.2019.10.01. eCollection 2020. Mediastinum. 2020. PMID: 35118272 Free PMC article. Review.
References
-
- Al-Assaf Yousef. Surface myoelectric signal analysis: dynamic approaches for change detection and classification. IEEE. Trans. Biomed. Eng, 53(11):2248–2256, 2006. - PubMed
-
- Alippi Cesare, Boracchi Giacomo, Carrera Diego, and Roveri Manuel. Change detection in multivariate datastreams: likelihood and detectability loss. In Proc. Int. Joint Conf. on Artif. Intelligence (IJCAI), 2016.
-
- Aminikhanghahi Samaneh and Cook Diane. Using change point detection to automate daily activity segmentation. In Proc. IEEE Int. Conf. on Perv. Comp. and Comm. Workshops (PerCom Workshops), 2017b.
-
- Andre-Obrecht Regine. A new statistical approach for the automatic segmentation of continuous speech signals. IEEE Trans. Accous. Speech. Signal Process, 36(1):29–40, 1988.
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
