The pucke.rs toolkit to facilitate sampling the conformational space of biomolecular monomers
- PMID: 40247410
- PMCID: PMC12007234
- DOI: 10.1186/s13321-025-00977-7
The pucke.rs toolkit to facilitate sampling the conformational space of biomolecular monomers
Abstract
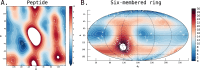
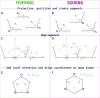
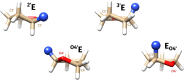
Understanding of the structural and dynamic behaviour of molecules is a major objective in molecular modeling research. Sampling through the torsional space is an efficient way to map their behaviour. However, generating a landscape of possible conformations relies on multiple formalisms whose mathematics are often difficult to convert to code. Here we present a command line tool and a scripting module to provide the means to generate such landscapes with different axes according to various formalisms exploited for conformational sampling. Additionally to this toolkit, we apply a benchmarking study on subjecting a DNA nucleoside to a diverse set of quantum mechanical levels of theory for geometry optimisations and energy potential calculations. The potential of the tool is demonstrated on examples including amino acids and synthetic nucleosides having five-membered or six-membered sugar moieties.
Keywords: Computational chemistry; Linear algebra; Puckering formalisms; Python; Rust.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The research group declares no conflicts of interest. The https://github.com/jrihon/puckers and the https://github.com/jrihon/puckepy are available on GitHub, where their documentation can be found as well. Installation procedures are given in the respective repositories, available for all major operating systems. Both tools are written in Rust, with pucke.py available as a Python library, and function under the MIT license. The Rust toolchain (cargo) solves dependencies, no Python dependencies required.
Figures
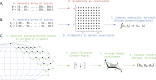
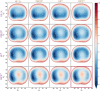


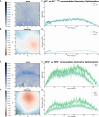
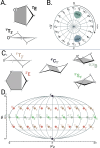
 level. Ranges from [0. 0.0010] Å. B. Energy difference between the PESs generated at the HF vs.
level. Ranges from [0. 0.0010] Å. B. Energy difference between the PESs generated at the HF vs.  level. Ranges from [-0.02 0.02]
C. RAM consumption required to produce a set of optimised structures at the HF vs.
level. Ranges from [-0.02 0.02]
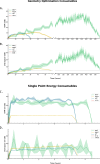
C. RAM consumption required to produce a set of optimised structures at the HF vs.  level. Whilst both top at around the same order of magnitude, it is baffling how well the RIJK optimisation approximates the Coulombic and Exchange Integrals by speeding up the wallclock time up to 800% ! D. Disk Space required to produce a set of optimised structures at the HF vs.
level. Whilst both top at around the same order of magnitude, it is baffling how well the RIJK optimisation approximates the Coulombic and Exchange Integrals by speeding up the wallclock time up to 800% ! D. Disk Space required to produce a set of optimised structures at the HF vs.  level. The explanation is analogous to the previous point made. E. RMSD between optimised conformers at the MP2 vs. MP2 level. Ranges from [0. 0.0010] Å. F. Energy difference between the PESs generated at the MP2 vs. MP2 level. Ranges from [-0.02 0.02]
G. RAM consumption required to produce a set of optimised structures at the MP2 vs. MP2 level. There is both little overall difference in the time spent calculating (± 550h vs. ± 500h) and the RAM required to run the calculation. H. Disk Space required to produce a set of optimised structures at the MP2 vs. MP2 level. Though there is a noticeable difference in stored tmp-files space, it does not feel like this can be a reason for opting for the TZVP basis set
level. The explanation is analogous to the previous point made. E. RMSD between optimised conformers at the MP2 vs. MP2 level. Ranges from [0. 0.0010] Å. F. Energy difference between the PESs generated at the MP2 vs. MP2 level. Ranges from [-0.02 0.02]
G. RAM consumption required to produce a set of optimised structures at the MP2 vs. MP2 level. There is both little overall difference in the time spent calculating (± 550h vs. ± 500h) and the RAM required to run the calculation. H. Disk Space required to produce a set of optimised structures at the MP2 vs. MP2 level. Though there is a noticeable difference in stored tmp-files space, it does not feel like this can be a reason for opting for the TZVP basis set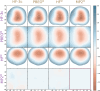


Similar articles
-
Efficient and Accurate Potential Energy Surfaces of Puckering in Sugar-Modified Nucleosides.J Chem Theory Comput. 2021 Jun 8;17(6):3814-3823. doi: 10.1021/acs.jctc.1c00270. Epub 2021 May 17. J Chem Theory Comput. 2021. PMID: 34000809
-
Seven-Membered Ring Nucleoside Analogues: Stereoselective Synthesis and Studies on Their Conformational Properties.Org Lett. 2015 Nov 6;17(21):5416-9. doi: 10.1021/acs.orglett.5b02769. Epub 2015 Oct 22. Org Lett. 2015. PMID: 26492193
-
Accurately Modeling the Conformational Preferences of Nucleosides.J Am Chem Soc. 2017 Oct 4;139(39):13620-13623. doi: 10.1021/jacs.7b07436. Epub 2017 Sep 25. J Am Chem Soc. 2017. PMID: 28899099
-
Computational methods for exploring protein conformations.Biochem Soc Trans. 2020 Aug 28;48(4):1707-1724. doi: 10.1042/BST20200193. Biochem Soc Trans. 2020. PMID: 32756904 Free PMC article. Review.
-
A comparative study of effective atomic number calculations for dual-energy CT.Med Phys. 2021 Oct;48(10):5908-5923. doi: 10.1002/mp.15166. Epub 2021 Aug 25. Med Phys. 2021. PMID: 34390593 Review.
References
-
- Zgarbová M, Šponer J, Otyepka M et al (2015) Refinement of the sugar-phosphate backbone torsion beta for amber force fields improves the description of z- and b-dna. J Chem Theor Comput 11(12):5723–5736. 10.1021/acs.jctc.5b00716 - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources

 /
/ conformers. Biophys J 92(11):3817–3829. 10.1529/biophysj.106.097782
-
conformers. Biophys J 92(11):3817–3829. 10.1529/biophysj.106.097782
-
