Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 Apr 23;15(1):14002.
doi: 10.1038/s41598-025-92144-z.

A statistical estimation of fractional order cryptosporidiosis epidemic model

Nauman Ahmed  1   2 , Wissal Audah Alhilfi  3 , Hanan A Z AlMansury  4 , Maysaa E A Elwahab  5 , Muhammad Tahir  1 , Ohud A Alqasem  5 , Zafar Iqbal  1 , Ali Raza  6 , Baboucarr Ceesay  7 , Muhammad Rafiq  8 , Ilyas Khan  9   10   11
Affiliations

A statistical estimation of fractional order cryptosporidiosis epidemic model

Nauman Ahmed et al. Sci Rep. .

Abstract

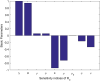
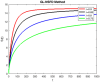
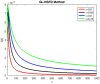
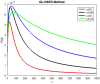
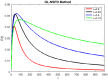
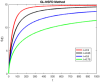
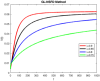
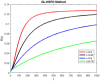
In this study, a statistical estimation is done for an epidemic model of cryptosporidiosis by changing it into a fractional order system. The disease-free equilibrium point, and the endemic equilibrium point are the two equilibrium points and Jacobian matrix theory is used to determine stability. The basic reproductive number [Formula: see text] is calculated and examined for its role in disease dynamics and stability analysis. The numerical technique named Grunwald Letnikov non-standard finite difference (GL-NSFD) scheme is designed for solving the fractional epidemic model. To investigate the characteristics and properties of numerical design, a test problem is considered for the simulation. For the underlying system, a non-classical numerical approach is suggested. The state variables cannot be negative because they describe the number of people. The suggested numerical scheme must have the properties of positivity and boundedness. The positivity and boundedness of the fractional order cryptosporidiosis epidemic model are investigated with the help of Laplace and inverse Laplace transformation. Finally, the conclusions of the study are elaborated.

Keywords: Boundedness; Fractional epidemic model; GL non-standard finite difference schemes; Positivity; Simulations; Statistical estimation.

PubMed Disclaimer

Conflict of interest statement

Declarations. Competing interests: The authors declare no competing interests. Ethical approval: Not available (No human/animal data is used here).

Figures

Fig. 1
Fig. 1
Sensitivity indices of parameter’s involved in reproduction number.
Fig. 2
Fig. 2
The graphs of susceptible population with different values of formula image.
Fig. 3
Fig. 3
The graphs of infected population with different values of formula image.
Fig. 4
Fig. 4
The graphs of recovered population with different values of formula image.
Fig. 5
Fig. 5
The graphs of microbial population with different values of formula image.
Fig. 6
Fig. 6
The graphs of susceptible population with different values of formula image.
Fig. 7
Fig. 7
The graphs of infected population with different values of formula image.
Fig. 8
Fig. 8
The graphs of recovered population with different values of formula image.
Fig. 9
Fig. 9
The graphs of microbial population with different values of formula image.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Riggs, M. W. Recent advances in cryptosporidiosis: The immune response. Microbes Infect.4(10), 1067–1080 (2002). - PubMed
    1. Tyzzer, E. E. A sporozoan found in the peptic glands of the common mouse. Proc. Soc. Exp. Biol. Med.5(1), 12–13 (1907).
    1. Nime, F. A., Burek, J. D., Page, D. L., Holscher, M. A. & Yardley, J. H. Acute enterocolitis in a human being infected with the protozoan Cryptosporidium. Gastroenterology70(4), 592–598 (1976). - PubMed
    1. Meisel, J. L., Perera, D. R., Meligro, C. & Rubin, C. E. Overwhelming watery diarrhea associated with a Cryptosporidium in an immunosuppressed patient. Gastroenterology70(6), 1156–1160 (1976). - PubMed
    1. Current, W. L. et al. Human cryptosporidiosis in immunocompetent and immunodeficient persons: Studies of an outbreak and experimental transmission. N. Engl. J. Med.308(21), 1252–1257 (1983). - PubMed