Competition between elasticity and adhesion in caterpillar locomotion

Abstract

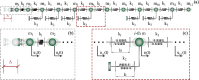
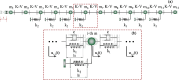
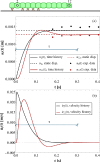
In recent years, there has been a growing interest in understanding animals' locomotion mechanisms for developing bio-inspired micro- or nano-robots capable of overcoming obstacles and navigating in confined environments. Among non-pedal crawlers, caterpillars exhibit one of the most stable and efficient gait strategies, utilizing muscle contractions and substrate grip. Although several approaches have been proposed to model their locomotion, little is known about the competition between body elasticity and adhesion, which we demonstrate playing a central role in crawling gait. Preliminarily, experimental observations and measurements were performed on Pieris brassicae larvae, gaining insights into fundamental features characterizing caterpillar locomotion and estimating key geometrical and mechanical parameters. A minimal but effective one-dimensional discrete model was thus conceived to capture all the relevant aspects of the movement. Inter-mass springs model the deformable body units, Winkler-like constraints with an adhesion threshold reproduce elastic interactions and attaching/detaching events at prolegs-substrate interface, and a triggering muscle contraction initiates the larva's crawling cycle, generating the observed travelling wave. After demonstrating theoretically that caterpillars move obeying quasi-static laws, we proved robustness of the proposed approach by showing very good agreement between theoretical outcomes and experimental evidence, so paving the way for new optimization strategies in soft robotics.

Keywords: caterpillar locomotion; crawling gait mechanics; interplay elasticity–adhesion.

Figure 1.

Evidence of caterpillar locomotion: in the left column, part (a), multiple crawling cycles captured by the Nikon D5600 camera are shown over a 29 s interval. During this time, a larva measuring 38 mm in length and weighing 0.35 g travels approximately 50 mm, achieving an average speed of about 1.7 mm s⁻¹. Using the red markers in part (a) as reference points for the larva’s current length, the corresponding stretch ratio (i.e. the current length divided by the resting length, $\lambda =L/L_0$) is plotted over time and provided in part (b). The stretch history is obtained by interpolating the data points, registered from video analysis via a capture and playback software and marked with a black circle, using a second-order polynomial. A prolonged stance phase is observed approximately from 5 to 11 s. Additionally, the stretch rate, $\dot{\lambda }$, reported in the form of a phase portrait versus $\lambda$ is provided by numerically deriving over time the stretch history and it is shown in part (c). In the central column, part (d), selected frames from a single crawling cycle (lasting 1.2 s) of a Pierris brassicae larva moving along a slender wooden element are presented. These frames, captured by the high-speed camera CMOS MINI FASTCAM AX100, highlight the progression of inelastic contraction as well as the sequential attachment and detachment of the prolegs, marked with red rectangles. Finally, in the right column, part (e), crawling sequences from the video [48] are presented to illustrate the walking behaviour of a different species.

Figure 2.

Sequence of snapshots capturing how the caterpillar probes the substrate through its thoracic legs (see the red arrows) before changing its locomotion verse. The images seem to highlight that the animal employs its anterior legs as sensors for testing the nature and the consistency of the substrate before initiating the movement.

Figure 3.

Morphological characteristics of the several subunits of caterpillars (Pierris brassicae species) observed through SEM: (a) terminal segment with the prolegs captured in the retracted phase (scale bar 1 mm), (b) abdominal segments (scale bar 2 mm) with a zoom, (c) highlighting the microstructures that act as section-cups and modulate adhesion on the substrate (scale bar 1 mm), (d) intermediate body units (scale bar 2 mm), (e) thoracic legs and head (scale bar 2 mm) with (f) an enlargement (scale bar 0.5 mm) focusing on the hooks-like legs probably adopting for testing the support before initiating locomotion. This figure synoptically collects the details of the anatomically different parts of the larva, each one corresponding to a specific function, as also specified in the dedicated literature [,–52].

Figure 4.

Measuring adhesion in caterpillar's abdominal prolegs: (a) experimental setup with high-speed camera registering the adhesion/detachment phases of the caterpillar on a wooden support; (b) details of the support and the ruler interposed between the camera and the substrate (the black arrow indicates the air flow ejected from the compressor that causes the caterpillar's detachment at 105 mm); (c, d) calibration and measurement of the force exerted by the air compressor, by calculating the deflection equal to 14 mm of a clamped steel beam (dimensions 62.5 × 4.43 × 0.25 mm and Young’s Modulus 210 × 10³ MPa); (e) snapshots captured by the camera of three states: in the first one, no air flow is applied and the caterpillar perfectly adheres to the surface, the second one reproduce an intermediate situation where an air force of 0.10 N loaded the prolegs, the third one is the frame where detachment occurs corresponding at a force of 0.20 N.

Figure 5.

Graphical representation showing the subsequent phases of the caterpillar's crawling gait: (a) resting phase, (b) activation of the locomotion through the inelastic contraction driven by the terminal proleg, (c) detachment of the first proleg when the threshold is achieved before the elastic repartition of the stress into the subsequent mechanical configuration. The direction and the verse of the motion is highlighted by the grey arrow. The parameter $m$ refers to the mass of the subunits, while $k_1$, $k_2$ and $k_3$ correspond to the stiffness of the body segments, the abdominal prolegs and the thoracic legs, respectively.

Figure 6.

Discrete lumped masses system adopted for modelling caterpillars' locomotion (a), where $k_1$ is the inter-masses springs' stiffness, while $k_2$ and $k_3$ are the Winkler-like springs' stiffness referring respectively to abdominal and thoracic legs; $l_0$ is the resting length and $m_i$ the $i$-th mass, representing the body segments of the caterpillar. The gray inset (b) provides detail on the posterior subunits, being the simple support modelling the terminal prolegs acting as pivot point with a prescribed displacement $\mathrm{\Delta }$ and the red rectangle (c) focuses on the $i$-th mass.

Figure 7.

Effects of the variation of the stiffness ratio $\alpha$, on the displacements solutions of each DoF (equation (3.3)), normalized with respect to ${\displaystyle \Delta }$. The parameters are set as ${\displaystyle \Delta \simeq 1.45\times {10}^{-3}\mathrm{m},{\mathrm{l}}_0=2.0\times {10}^{-3}\mathrm{m},\alpha =0.01,{\mathrm{u}}_{\mathrm{y}}={\mathrm{l}}_0/1.5=1.33\times {10}^{-3}\mathrm{m},{\mathrm{k}}_1=5\mathrm{N}{\mathrm{m}}^{-1}}$. While the geometric and the mass parameters have been experimentally measured, the stiffness $k_1$ has been evaluated starting from the findings of the research paper [26], where the Young’s modulus of the caterpillar muscle tissue is estimated approximately ${\displaystyle 2.5\mathrm{k}\mathrm{P}\mathrm{a}}$..

Figure 8.

Illustration reproducing the substeps that occur during caterpillar locomotion with the progressive detachment of prolegs: the stance phase is depicted in configuration (a), while configuration (b.1) reports the substep 1, where the loss of adhesion of the Winkler-like spring is achieved at the threshold $u_y$ provided in inset (b.2); part (c), (d) and (e) refer to the subsequent substeps where the two adjacent constraints that modulate the substrate interaction attain the detachment force. This gait continues up to the last proleg is detached, by completing one crawl-cycle and by leading the whole body to move of ${\displaystyle \Delta }$ (substep 4).

Figure 9.

A qualitative comparison of the morphological features of some caterpillar species, i.e. Pierris brassicae (a), Uresiphita gilvata (b), Amphipyra pyramidea (c) and Papilio machaon (d) is provided, recalling how variations in geometric parameters and body/prolegs elasticity can influence gait triggering action. To highlight this, part (e) reports a region plot in logarithmic scale analysing the possible combinations of parameters of the linear system, by highlighting when locomotion is made possible: the dimensionless ratio ${\displaystyle \tilde{\Delta }/u_y}$ is provided as a function of the stiffness ratio $\alpha$. The inset in part (e) reports a zoom on the range of low stiffness ratios. In detail, the ${\displaystyle \tilde{\Delta }/u_y}$ parameter represents the ratio between the inelastic contraction to be applied for triggering locomotion and the threshold displacement for detaching prolegs, which somehow quantifies the energy needed to activate and to maintain locomotion with respect to the elastic energy cumulated in the Winkler-like springs before detaching from the substrate. The grey area refers to incompatible values, where interpenetration between adjacent masses occurs, while the admissible states are included in the complementary zone. By recalling that ${\displaystyle \tilde{\Delta }}$ must be $\le l_0$ for avoiding interpenetration between the first and the subsequent body segment, one can fix—as a limit case—the ratio $l_0/u_y$ depending on the analysed caterpillar species, and a priori evaluate the optimal stiffness ratio value that minimizes the input energy of the larva for achieving and maintaining locomotion (see the blue circle on the black curve). The dimensionless parameter $l_0/u_y$ characterises the relation between the resting length of the body units and the displacement threshold of the Winkler-like constraints, thereby defining a geometric ratio that may play a crucial role in the evolutionary dynamics of caterpillars. Moreover, by selecting a prescribed stiffness ratio, we can predict the minimum inelastic displacement ${\displaystyle \tilde{\Delta }}$ that initiates and maintains stable the locomotion (see the red circle on the black curve). The point related to the numerical simulations illustrated in this work is marked with a green circle.

Figure 10.

Numerical example of the elasto-static solutions in the linear elasticity framework: displacement values $u_i$ as a function of the $i$-th DoF at all substeps (a) and a graphical representation of them by highlighting the attachment/detachment of the prolegs depicted through brown triangles (b). At the fifth step, the caterpillar achieves its final position, thus translating each DoF of ${\displaystyle \tilde{\Delta }\simeq 1.45\times {10}^{-3}\mathrm{m},\text{being instead}{\mathrm{l}}_0=2.0\times {10}^{-3}\mathrm{m},\alpha =0.01,{\mathrm{u}}_{\mathrm{y}}={\mathrm{l}}_0/1.5=1.33\times {10}^{-3}\mathrm{m},\text{and }{\mathrm{k}}_1=5\mathrm{N}{\mathrm{m}}^{-1}}$.

Figure 11.

Elasto-static solutions of the caterpillar locomotion varying $\alpha$: displacement values $u_i$ as a function of the $i$-th DoF at all substeps. For all the plots these parameters are fixed: ${\displaystyle \tilde{\Delta }\simeq 1.45\times {10}^{-3}\mathrm{m},{\mathrm{l}}_0=2.0\times {10}^{-3}\mathrm{m}\text{and}{\mathrm{k}}_1=5\mathrm{N}{\mathrm{m}}^{-1}}$. The displacement threshold $u_y$ is modulated in order to keep invariant the triggering ${\displaystyle \tilde{\Delta }}$ calculated as made explicit in (3.5), therefore, the following parameters are assumed: ${\displaystyle \alpha =0.05,u_y\simeq 1.0e-3\mathrm{m}(\text{a}),\alpha =0.1,u_y\simeq 8.1e-4\mathrm{m}(\text{b}),\alpha =1,u_y\simeq 2.1e-4\mathrm{m}(\text{c}),\alpha =10,u_y\simeq 2.8e-5\mathrm{m}(\text{d})}$.

Figure 12.

Discrete dynamic lumped masses model adopted for modelling caterpillar locomotion and accounting for the viscosity of the cuticle/muscle tissue through linear dashpots, whose damping coefficient is appointed as $c$, placed in parallel to inter-masses springs, thus obtaining several Kelvin-Voigt (K-V) links in series (b). Winkler-like springs are still considered for modulating the caterpillar-substrate interaction.

Figure 13.

By assuming the following set of parameters ${\displaystyle m=1\times {10}^{-4}\mathrm{k}\mathrm{g},{\mathrm{l}}_0=2\times {10}^{-3}\mathrm{m},{\mathit{u}}_{\mathit{y}}=1.33\times {10}^{-3}\mathrm{m},{\mathrm{k}}_1=5\mathrm{N}{\mathrm{m}}^{-1},\alpha =0.01,\tilde{\Delta }=1.45\times {10}^{-3}\mathrm{m}}$ and $\xi =5$, comparison among dynamic analyses, elasto-static solutions and experimental data: (a) displacement histories $u_2(t)$ and $u_{12}(t)$ compared with the corresponding solutions of the elasto-static problem and experimental data of the displacement of the ${\displaystyle 2^{\mathrm{n}\mathrm{d}}}$ and ${\displaystyle {12}^{\mathrm{t}\mathrm{h}}}$ body segment at the end of the first crawl-substep, (b) velocity histories of the same selected DoFs, being $\tau$, for both plots, the duration of the transient phase.