Exploring the Evolution-Coupling Hypothesis: Do Enzymes' Performance Gains Correlate with Increased Dissipation?

Abstract

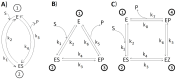
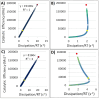
The research literature presents divergent opinions regarding the role of dissipation in living systems, with views ranging from it being useless to it being essential for driving life. The implications of universal thermodynamic evolution are often overlooked or considered controversial. A higher rate of entropy production indicates faster thermodynamic evolution. We calculated enzyme-associated dissipation under steady-state conditions using minimalistic models of enzyme kinetics when all microscopic rate constants are known. We found that dissipation is roughly proportional to the turnover number, and a log-log power-law relationship exists between dissipation and the catalytic efficiency of enzymes. "Perfect" specialized enzymes exhibit the highest dissipation levels and represent the pinnacle of biological evolution. The examples that we analyzed suggested two key points: (a) more evolved enzymes excel in free-energy dissipation, and (b) the proposed evolutionary trajectory from generalist to specialized enzymes should involve increased dissipation for the latter. Introducing stochastic noise in the kinetics of individual enzymes may lead to optimal performance parameters that exceed the observed values. Our findings indicate that biological evolution has opened new channels for dissipation through specialized enzymes. We also discuss the implications of our results concerning scaling laws and the seamless coupling between thermodynamic and biological evolution in living systems immersed in out-of-equilibrium environments.

Keywords: catalytic efficiency; dissipation; entropy production; evolution; generalist enzymes; kinetic constants; scaling laws; specialized enzymes; stochastic noise; turnover number.

Figure 1

Reversible kinetic schemes for transitions among functionally important enzyme conformations. We assumed predominantly counterclockwise cycling among states E (1), ES (2), EP or EZ (3), and EP (3 or 4). Forward kinetic constants are k₁, k₃, k₅, and k₇. The reverse kinetic constants are k₂, k₄, k₆, and k₈. (A) Two-state scheme. (B) Three-state scheme. (C) Four-state scheme. We multiplied the second-order rate constants by the substrate or product concentration to obtain k₁ and k₄ in panel (A), k₁ and k₆ in panel (B), and k₁ and k₈ in panel (C). In this way, all rate constants are expressed in the units of inverse seconds (first-order rate constants).

Figure 2

Multi-colored results for the main enzyme classes (EC numbers). Enzyme names are available in Table 1. Corresponding references are available in Dataset S1. (A) We illustrate a roughly linear relationship between entropy production (dissipation) and catalytic constant (k_cat) for 58 enzyme-catalyzed reactions from our database. (B) The right-hand panel exhibits the power-law relationship with the 0.73 exponent between the dissipation and enzyme efficiency (k_cat/K_m) for the same reaction set. The determination coefficient values of 0.89 (A) and 0.92 (B) indicate a good-to-solid fit in a linear regression model for the log-transformed data. The 95% confidence interval (CI) for the exponent is (0.87, 1.05) for (A) and (0.67, 0.78) for (B). These results mean that the exponent is reliably close to 0.96 (A) and 0.73 (B), with high confidence that the relationship between enzyme performance and dissipation follows a power law with an exponent in this range. The sensitivity analysis using the bootstrap method yielded a mean exponent of 0.731, a standard deviation of 0.033, and a 95% CI range of 0.67–0.80 for the (B) regression line. The diffusion limit range (pink rectangle) from (B) starts from 10⁸ (Ms)⁻¹. It highlights several specialized enzymes (see the main text) that reached the pinnacle of their evolutionary development for their catalytic efficiency and associated high entropy production. Seven generalist enzymes are among those catalyzing the 20 reactions with the lowest dissipation (less than 6 s⁻¹ dissipation/RT), and only one is among the enzymes catalyzing the 20 reactions with the highest dissipation. The chosen colors are red for isomerases (EC 5.2.1.8, 5.3.1.-, and 5.3.3.1), green for racemases (EC 5.1.1.-, and 5.1.2.2), dark olive green for epimerases (EC 5.1.1.21, and 5.1.3.-), olive for mutases (EC 5.4.2.1, 5.4.3.6, and 5.4.99.-), pink for kynureninases (EC 3.7.1.3), psychedelic purple for β-galactosidases (EC 3.2.1.23), purple for β-lactamases (EC 3.5.2.6), yellow for fumarate hydratases (EC 4.2.1.2), orange for carbonic anhydrases (EC 4.2.1.1), bronze for soluble inorganic pyrophosphatases (EC 3.6.1.1), blue for (R)-selective amine transaminases (EC 2.6.1.21), and black for kinesin-1 (EC 5.6.1.3).

Figure 3

Experimentally observed and simulation results for medically important variants of human kynureninase [47]: the generalist variant HsKYNase_93D9 (A,B), and the specialized variant HsKYNase_66 (C,D). The dissipation calculated for the specialist variant from the observed data is double that of the generalist variant (compare yellow points in the upper and lower panels). The simulations using forward variations (A,C) illustrate an almost vertical linear increase in the enzyme efficiency k_cat/K_m for small changes in the dissipation/RT values when all forward rate constants are subject to the same random noise within the restriction that the equilibrium constants K_i do not change in the simulation steps. The yellow and red points represent the observed and maximal k_cat/K_m values, respectively. The trade-off variations provided different results (B,D). The maximum entropy production requirement for the trade-off between enzyme–substrate association and enzyme–product dissociation rate within the framework of fixed total force almost doubled the optimal enzyme efficiency ((B), light pink point) with respect to the observed value ((B), yellow point) for the generalist variant. For the specialized variant, trade-off variations resulted in a smaller optimal k_cat/K_m value ((D), light pink point) with respect to the observed value ((D), yellow point). The yellow and red points have the same meaning and similar k_cat/K_m values as in (A,C).

Figure 4

Molecular phylogenetic tree and calculation of evolutionary distances by maximum likelihood method for β-lactamases PC1, RTEM, and Lac1 [96] after using the corrected sequence of Lac1 [95]. Summing all relevant branch lengths (number above each branch leading to the label “Ambler sequence” in red color) gives the following results in evolutionary distances: 1.19 for PC1, 1.44 for RTEM, and 1.60 for Lac1 (reproduced from [17]).

Figure 5

The performance parameters and evolutionary distances (from a common ancestor) of three β-lactamases: PC1 from S. aureus, RTEM from E. coli, and Lac1 from B. cereus. The increase in the evolutionary distance PC1 = 1.19 < RTEM = 1.44 < Lac-1 = 1.60 [16,19] is associated with the higher dissipation (A), catalytic constant (B), enzyme efficiency (C), and optimal k_cat that we derived from the maximal entropy production requirement (D). The PC1 (x,y) parameters define the lowest, RTEM the middle, and Lac-1 the highest point in all four panels.