Information Theory in Perception of Form: From Gestalt to Algorithmic Complexity

Abstract

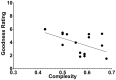
In 1948, Claude Shannon published a revolutionary paper on communication and information in engineering, one that made its way into the psychology of perception and changed it for good. However, the path to truly successful applications to psychology has been slow and bumpy. In this article, we present a readable account of that path, explaining the early difficulties as well as the creative solutions offered. The latter include Garner's theory of sets and redundancy as well as mathematical group theory. These solutions, in turn, enabled rigorous objective definitions to the hitherto subjective Gestalt concepts of figural goodness, order, randomness, and predictability. More recent developments enabled the definition of, in an exact mathematical sense, the key notion of complexity. In this article, we demonstrate, for the first time, the presence of the association between people's subjective impression of figural goodness and the pattern's objective complexity. The more attractive the pattern appears to perception, the less complex it is and the smaller the set of subjectively similar patterns.

Keywords: algorithmic complexity; gestalt; information; redundancy; sets.

Figure 1

Two dot patterns defined by their R & R subsets and their symmetry groups. (Left panel): Size of the R & R subset = 1; size of symmetry group = 8 [I, V, H, L, R, 90°, 180°, and 270° rotations]. (Right panel): Size of the R & R subset = 8; similarity group = 1 [I]. I: identity; V: vertical reflection; H: horizontal reflection; L: left-diagonal reflection; R: right-diagonal reflection. Based on [2,19].

Figure 2

Total set of 8 stimuli formed by crossing the binary values of 3 dimensions: form (circle, square) × slope (upwards, downwards) x line (solid, broken) (based on [21]).

Figure 3

A subset of 4 stimuli drawn from the total set of Figure 2. Notice the correlation between line and slope: with solid lines, the slope is upward, whereas with broken lines, the slope is downward. All subsets must contain redundancy or correlation.

Figure 4

A pair of well known images of public institutions and systems. Notice the appreciable amounts of symmetry, hence little information, in each symbol. They are easily perceived, recognized, and remembered.

Figure 5

Average LZ complexity as a function of the R & R subset.

Figure 6

Judged figural goodness of a pattern as a function of the pattern’s complexity as assessed by SubSym. The ratings of figural goodness were taken from [27]. The Pearson correlation between the two variables is −0.54.