Optimal vaccination model of airborne infection under variable humidity and demographic heterogeneity for hybrid fractional operator technique
- PMID: 40287448
- PMCID: PMC12033365
- DOI: 10.1038/s41598-025-93346-1
Optimal vaccination model of airborne infection under variable humidity and demographic heterogeneity for hybrid fractional operator technique
Abstract
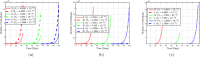
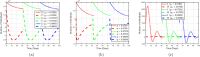
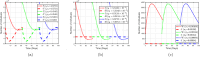
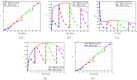
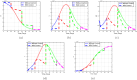
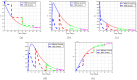
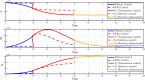
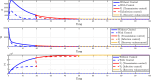
Airborne respiratory tract infection typically occurs seasonally in subtropical countries, particularly during winter, when transmission and fatality rates considerably rise, indicating that low humidity and freezing temperatures facilitate the transmission of viral strains in age heterogeneity. Despite this, the atmospheric elements that contribute to periodic influenza occurrences and their critical influence on the spread of influenza stay ambiguous in various age groups. The oversight of undetected cases amid a widespread outbreak of transmissible illnesses results in an underappreciation of the prevalence of infection and the basic recurrence rate. This study proposes the dynamics of the influenza epidemic in the province of Madrid, Spain, with an emphasis on the effects of control employing actual data. The main challenge is accurately estimating the virus's rate of transmission and assessing the effectiveness of vaccination campaigns. By taking into account the modified Atangana-Baleanu-Caputo (mABC) fractional difference operator, we develop an analytical framework for an outbreak caused by influenza and broaden it to accommodate the fractional scenario. The non-negativity and boundedness are guaranteed by the computation of the fractional-order influenza system. At the disease-free equilibrium (DFE), we perform a local asymptotic stability analysis (LAS) and display the outcome for [Formula: see text]. In addition, periodic solutions and the model's uniform permanence are proved. Environmental factors to decrease interaction between different ages, increase immunization protection, and minimize vaccine refusal risks are the most efficient way to meet preventative and surveillance targets. Our system's best-fit parameter settings were detected using the Markov Chain Monte Carlo (M-C-M-C) technique with influenza information collected in Spain. We predict a basic reproduction number of 1.3645 (96% C.I: (1.3644, 1.3646)). The framework's essential variables are determined using unpredictability and sensitivity evaluation. To further bolster the operator's effectiveness, a number of tests of this novel kind of operator were conducted. We remark that in various time scale domains [Formula: see text], the investigated discrete formulations will be [Formula: see text]-nonincreasing or [Formula: see text]-nondecreasing by examining [Formula: see text]-monotonicity formulations and the basic properties of the suggested operator. Algorithms are constructed in the discrete generalized Mittag-Leffler (GML) kernel for mathematical simulations, emphasizing the effects of the infection resulting from multiple factors. The dynamical technique used to build the influenza framework was significantly impacted by fractional-order. In order to lessen the infections, time-dependent control factors are also implemented. The optimality criteria are produced by applying Pontryagin's maximal argument to prove the validity of the most effective control. If vaccine penetration and immunity rates have been resurrected, achieving the control objective requires 12 months longer and costs less than the previous scenario.
Keywords: Airborne respiratory tract infection; Lyapunov functional; Modified Atangana-Baleanu-Caputo fractional operator; Numerical and epidemiological modeling; Optimum control; Parameter estimation; Vaccination.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare no competing interests.
Figures






Similar articles
-
Dynamic analysis and optimal control of a hybrid fractional monkeypox disease model in terms of external factors.Sci Rep. 2025 Jan 23;15(1):2944. doi: 10.1038/s41598-024-83691-y. Sci Rep. 2025. PMID: 39848956 Free PMC article.
-
Vaccines for preventing influenza in healthy children.Cochrane Database Syst Rev. 2018 Feb 1;2(2):CD004879. doi: 10.1002/14651858.CD004879.pub5. Cochrane Database Syst Rev. 2018. PMID: 29388195 Free PMC article.
-
Vaccines for preventing influenza in healthy adults.Cochrane Database Syst Rev. 2018 Feb 1;2(2):CD001269. doi: 10.1002/14651858.CD001269.pub6. Cochrane Database Syst Rev. 2018. PMID: 29388196 Free PMC article.
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
-
Vaccines for preventing influenza in the elderly.Cochrane Database Syst Rev. 2018 Feb 1;2(2):CD004876. doi: 10.1002/14651858.CD004876.pub4. Cochrane Database Syst Rev. 2018. PMID: 29388197 Free PMC article.
References
-
- Hutchinson, E. C. Influenza virus. Trends Microbiol.26, 809–810 (2018). - PubMed
-
- World Health Organization. Recommended composition of influenza virus vaccines for use in the 2023-2024 northern hemisphere influenza season. Available at https://www.who.int/publications/m/item/recommended-composition-of-influ... (accessed 31 December 2023).
-
- Instituto de Salud Carlos III. Sistema de Vigilancia de Gripe en España. Informes anuales, temporadas 1999/2000-2019-2020 (Influenza Surveillance in Spain. Annual reports, seasons 1999/2000-2019-2020). Available at https://www.isciii.es/QueHacemos/Servicios/VigilanciaSaludPublicaRENAVE/...
-
- Yin, D. et al. Dendritic-cell-targeting virus-like particles as potent mRNA vaccine carriers. Nat. Biomed. Eng.10.1038/s41551-024-01208-4 (2024). - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Medical

