Viscoelastic friction in sliding a non-cylindrical asperity

Abstract

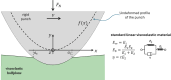
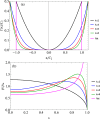
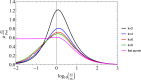
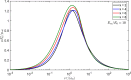
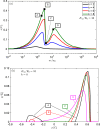
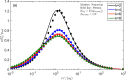
We investigate the 2D contact problem of sliding a non-cylindrical punch on a viscoelastic halfplane, assuming a power law shape ${\left(x\right)}^k$ with $k>2$ . We find with a full boundary element numerical solution that the Persson analytical solution for friction, which works well for the cylindrical punch case assuming the pressure remains identical in form to the elastic case, in this case leads to significant qualitative errors. However, we find that the friction coefficient follows a much simpler trend; namely, we can use as a first approximation the solution for the cylinder, provided we normalize friction coefficient with the modulus and mean pressure at zero speed, despite that we show the complex behaviour of the pressure distribution in the viscoelastic regime. We are unable to numerically solve satisfactorily the ill-defined limit of sharp flat punch, for which Persson's solution predicts finite friction even at zero speed.

Fig. 1

Schematic of the 2D power law profile sliding over a linear viscoelastic halfplane. We assume the punch has thickness L in the z direction. A schematic for a standard linear viscoelastic material is shown in the Kelvin representation where $\{E_1,E_2\}$ have the dimension of an elastic modulus, $\eta$ is the viscosity and $\tau$ is the characteristic time of the material. $\{a_l,a_t\}$ are the contact semi-widths, respectively, at the leading and trailing edge. In the elastic limit (very low or very high sliding velocity) $|a_l|=|a_t|$

Fig. 2

a Profiles of the power law punches considered in this study $f(x)=\frac{{\left|x\right|}^k}{k{C}_2^{k-1}}$ and of a flat punch, shown in dimensionless form. b The dimensionless (elastic) pressure distribution $\frac{p\left(s\right)}{p_m}=\frac{p_0\left(s\right)}{p_{m0}}$ as in Eq.(12) as function of the dimensionless coordinate $s=x/a$ for power law punch for $k=2,4,6,8$ and the limit flat punch solution, respectively, black, blue, red, green, and purple curves. Notice that this pressure also holds for viscoelastic case for very low speed

Fig. 3

Using Persson’s solution [22] for a power law punch in terms of $\mu E_0^{\ast }/p_{m0}$ as a function of the dimensionless velocity $v\tau /a_0,$ assuming “elastic” pressure distribution, for $k=\left[2,,,4,,,6,,,8\right]$ and the limit flat punch solution, respectively, black, blue, red, green, and purple curves

Fig. 4

BEM solution for $\mu E_0^{\ast }/p_{m0}$ for power law punch for $k=\left[2,,,4,,,6,,,8\right]$

Fig. 5

The pressure distribution obtained from BEM solution for $v\tau /a_0=1.504$ for power law punch for $k=\left[2,,,4,,,6,,,8\right]$

Fig. 6

a The eccentricity of the pressure distribution $e/C_2$ calculated with Eq. (16) using the pressure distribution obtained numerically with the BEM code as function of $v\tau /a_0$ for power law punch for $k=\left[2,,,4,,,6,,,8\right]$. b The pressure distributions for the sliding velocities $v\tau /a_0=\left[1.89,,,3.00,,,3.78,,,11.94\right]$ and $k=8$ (labelled (A, B, C, D)) are shown

Fig. 7

$\mu E_0^{\ast }/p_{m0}$ as a function of the dimensionless velocity $v\tau /a_0$ for Persson’s solution [22] (solid lines) compared with the curves that can be obtained numerically assuming the pressure distribution remains symmetrical and “elastic” but using an effective modulus $E_{\mathit{eff}}^{\ast }\left({\beta }_{\mathit{Persson}},\frac{v}{a}\right)$ that satisfies Eq. (17) $\left({\beta }_{\mathit{Persson}},\simeq ,\pi ,/,2\right)$