Evolutionary dynamics of behavioral motivations for cooperation

Abstract

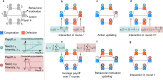
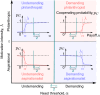
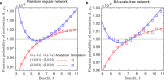
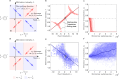
Human decision-making is shaped by underlying motivations, which reflect both subjective well-being and fundamental biological needs. Different needs are often prioritized and traded off against one another. Here we develop a theoretical framework to study the evolution of behavioral motivations, encompassing both philanthropic (cooperating after personal needs are met) and aspirational (cooperating to fulfill personal needs) motivations. Our findings show that when the ratio of benefits to costs for cooperation exceeds a critical threshold, individuals initially driven by aspirational motivations can transition to philanthropic motivations with a low reference point for cooperation, resulting in increased cooperation. Furthermore, the critical threshold depends on the structure of the underlying social network, with network modifications capable of reversing the evolutionary trajectory of motivations. Our results reveal the complex interplay between needs, motivations, social networks, and decision-making, offering insights into how evolution shapes not only cooperative behaviors but also the motivations behind them.

Fig. 1. Evolutionary dynamics of behavioral motivation.

a The population structure is described by a network, and each individual (node) in the population has a behavioral motivation A or B (circle) and adopts action cooperation (C) or defection (D) (square). The figure illustrates two examples of behavioral motivations: one with need α_A and motivation intensity λ_A, and the other with need α_B and motivation intensity λ_B. With the shown behavioral motivation A, the individual is more likely to cooperate when his payoff exceeds the need, i.e., u > α_A. Conversely, with the shown behavioral motivation B, the individual tends to defect when he fulfills his needs, i.e., u > α_B. b In every round t, every individual adopts cooperation or defection to play games with each neighbor and obtain an edge-weighted average payoff u_i(t). Here we consider a network where all edge weights are set to 1. c An individual (marked by “?”) is selected uniformly at random to update his action based on his own behavioral motivation, namely, to cooperate next round with the cooperating probability and to defect otherwise. d Game playing and action updates repeat in the next round, t + 1. e After T rounds of interactions, individuals obtain an average payoff, ${ū}_i={\sum }_{t=1}^T{u}_i\left(t\right)/T$. f An individual (marked by “?”) is selected uniformly at random to update his behavioral motivation, and all neighboring individuals, indicated by black circles, compete to be imitated by the focal individual, with probability proportional to their average payoff. g After the behavioral motivation updating, game playing, and action updates restart from round 1.

Fig. 2. Four representative behavioral motivations.

A behavioral motivation is described by a pair of variables, namely need threshold (α) and motivation intensity (λ), corresponding to a point in the (α, λ) plane. In a donation game, if both participants choose cooperation (or defection) with probability 0.5, each player’s expected payoff is (b − c)/2. If a player’s need threshold is greater than (b − c)/2, they are referred to as ‘demanding’, whereas they are referred to as ‘undemanding’ if their need threshold is less than (b − c)/2. If a player’s motivation intensity λ has a positive value, this indicates that they are more likely to cooperate if their need is met, which we call ‘philanthropic’ behavioral motivation. If λ is negative, they are more likely to cooperate if their need is not met, which we refer to as ‘aspirational’ behavioral motivation. As such, there are four qualitatively different types of players: undemanding philanthropist, demanding philanthropist, undemanding aspirationalist, and demanding aspirationalist.

Fig. 3. Undemanding philanthropic and demanding aspirational behavioral motivations promote cooperation.

We consider four types of games, namely two-action donation games (a, e), three-action linear donation games (b, f), three-action nonlinear donation games with benefit factor ω = 1.5 (c, g), and with benefit factor ω = 0.5 (d, h). Dots in (a–d) illustrate the optional actions in the game, with the action cost shown in the x-axis and the generated benefit in the y-axis. e–h presents the abundance of cooperation as the average need threshold $\overline{\alpha }$ varies from undemanding to demanding levels. In each game, we investigate both philanthropic (blue, λ = 0.01) and aspirational (red, λ = −0.01) behavioral motivations on six classes of networks (random regular networks (RR), Erdös-Rényi networks (ER), Watts-Strogatz small-world networks (SW) with rewiring probability 0.1, Barabási-Albert scale-free networks (BA-SF), Goh-Kahng-Kim scale-free networks (GKK-SF) with exponent 2.5, and Holme-Kim scale-free networks (HK-SF) with triad formation probability 0.1). Dots in (e–h) indicate the results of Monte Carlo simulations, and lines are analytical results. The results show that in a population of undemanding philanthropic and demanding aspirational behavioral motivations, cooperation is favored, consistent in all population structures. Each dot in (e–h) is the result averaged over 5000 simulations, and each simulation lasts for 10⁵ rounds. We consider two initial configurations: individuals occupying the largest 50% of highly connected nodes have a higher threshold, α + ϵ, while those in the least 50% have a lower threshold, α − ϵ (positive correlation, solid dots); individuals in the largest 50% of highly connected nodes have a lower threshold, α − ϵ, and those in the least 50% have a higher threshold, α + ϵ (negative correlation, open dots). Parameter values: network size N = 100, average degree d = 6, benefit b = 6, cost c = 1, and ϵ = 0.5.

Fig. 4. Breaking down a high level of need into small pieces can make cooperation favorable.

a Abundance of cooperation x_C as a function of the need threshold α and the number of available actions L in the multi-action linear donation game. In the red zone, the cooperation abundance x_C decreases monotonously with L, and a large L can make cooperation less favorable. In the blue zone, the increasing L monotonously increases the cooperation abundance x_C. The solid dashed line marks the level of x_C = 1/2. Thus, for behavioral motivations with a high need threshold α > 1/2, increasing the number of available actions can make cooperation favorable, i.e., x_C > 1/2. b Abundance of cooperation x_C as a function of the benefit factor ω and the number of available actions L in the multi-action nonlinear donation game. Generally, the cooperation abundance increases with L for ω < 1 and decreases with L for ω > 1. Similarly, for ω < 1, increasing the number of available actions can make cooperation favorable, i.e., x_C > 1/2. Parameter values: b = 6, c = 1, λ = 0.01, and α = 3 (b).

Fig. 5. Selection favors undemanding philanthropists over demanding philanthropists when the benefit-to-cost ratio exceeds a critical value.

Presented is the fixation probability of an individual using behavioral motivation A, i.e., (α_A, λ_A), in the population of individuals using behavioral motivation B, i.e., (α_B, λ_B), as a function of benefit b in the two-action donation game, with cost c = 1. We consider random regular networks (a) and BA scale-free networks (b). Selection favors behavioral motivation A over B if fixation probability ρ_A exceeds the horizontal line, i.e., ρ_A > 1/N. Squares indicate fixation probabilities by Monte Carlo simulations, and solid lines are analytical results. Red lines and squares represent the fixation probability of philanthropic motivation A, i.e., (1,0.01), in a population of B, i.e., (3,0.01), which shows that selection favors undemanding over demanding individuals as long as the benefit-to-cost ratio exceeds the critical ratio, i.e., b/c > (b/c)^*. Nonetheless, for motivations with α_A = α_B, the evolution of the motivation intensity is non-monotonous with benefit b --- both the small and large b/c favor a strong motivation, while the intermediate b/c favors weak motivation, as blue lines and dots show (the evolution of (2,0.03) in a population of (2,0.01)). The fixation probability of beneficial motivation A, ρ_A, is determined by the fractions of simulations where the beneficial motivation A reached fixation out of 2 × 10⁷ generations. Parameter values: population size N = 100 and average degree d = 6.

Fig. 6. Evolution of behavioral motivation.

a The theoretical prediction of the evolutionary direction of behavioral motivations for (b/c) < (b/c)^*. The evolution results in individuals transitioning away from undemanding philanthropists (region II) and demanding aspirationalists (region IV), and towards demanding philanthropists (region I) and undemanding aspirationalists (region III), as indicated by the arrows. This transition leads to a decrease in the abundance of cooperation x_C. The blue (respectively red) regions represent the behavioral motivation that contributes to a larger abundance of cooperation than defection (respectively defection than cooperation). b The Monte Carlo simulations show the evolutionary trajectories of behavioral motivations for (b/c) < (b/c)^* using 300 simulations in random regular networks. Each simulation starts from a monomorphic population with behavioral motivations (α, λ) in one of (0.75,0.05), (0.25,0.05), (0.25,− 0.05), and (0.75,− 0.05), represented by open black dots, and undergoes 5 × 10⁷ motivation updating steps, where interactions and action updates repeat for T = 100 rounds before each motivation updating. During each behavioral motivation update, with a probability of 0.01, the imitated behavioral motivation is subject to a random fluctuation in need α (randomly sampled from the range [− 0.1,0.1]) and motivation intensity λ (randomly sampled from the range [− 0.01,0.01]). Each thin red line represents a resulting trajectory (i.e., the average behavioral motivation of the population), and each open red dot represents an ending behavioral motivation. The thick red line represents the linear regression of all final behavioral motivations, which is highly consistent with the evolutionary direction predicted analytically in (a). c The cooperation abundance throughout the evolutionary process (b/c) < (b/c)^* by simulations. The highlighted line represents the average cooperation abundance over the 300 simulations. d The theoretical prediction of the evolutionary direction of behavioral motivations for (b/c) > (b/c)^* shows that individuals evolve towards undemanding philanthropists (region II) and demanding aspirationalists (region IV). e The evolutionary trajectories of behavioral motivations for (b/c) > (b/c)^* by simulations. f The cooperation abundance throughout the evolutionary process for (b/c) > (b/c)^* by simulations. Parameter values: N = 100, d = 6, which gives (b/c)^* ≈ 6.7, b = 2, c = 1 (bc) and c = 0.2 (ef).