Multi-messenger gravitational lensing

Abstract

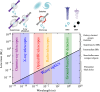
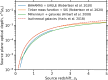
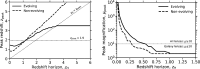
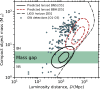
We introduce the rapidly emerging field of multi-messenger gravitational lensing-the discovery and science of gravitationally lensed phenomena in the distant universe through the combination of multiple messengers. This is framed by gravitational lensing phenomenology that has grown since the first discoveries in the twentieth century, messengers that span 30 orders of magnitude in energy from high-energy neutrinos to gravitational waves, and powerful 'survey facilities' that are capable of continually scanning the sky for transient and variable sources. Within this context, the main focus is on discoveries and science that are feasible in the next 5-10 years with current and imminent technology including the LIGO-Virgo-KAGRA network of gravitational wave detectors, the Vera C. Rubin Observatory and contemporaneous gamma/X-ray satellites and radio surveys. The scientific impact of even one multi-messenger gravitational lensing discovery will be transformational and reach across fundamental physics, cosmology and astrophysics. We describe these scientific opportunities and the key challenges along the path to achieving them. This article therefore describes the consensus that emerged at the eponymous Theo Murphy meeting in March 2024, and also serves as an introduction to this Theo Murphy meeting issue.This article is part of the Theo Murphy meeting issue 'Multi-messenger gravitational lensing (Part 2)'.

Keywords: gamma-ray burst; gravitational lensing; gravitational waves; kilonova; multi-messenger astronomy; time domain astronomy.

Figure 1.

Illustration of the mass scales at which wave optics effects become relevant for gravitationally lensed signals. The geometric optics regime is valid when the wavelength of the radiation is much smaller than the scale of the lensing potential. The wave optics regime is valid when the wavelength is comparable to the scale of the lensing potential. Because the wavelength of GWs detected by the current ground-based detectors is typically much larger than the wavelength of most light sources, wave optics effects can become relevant for lenses below $\lesssim 100{\mathrm{M}}_{\odot }$. Since other GW detectors like LISA will be sensitive to even longer wavelengths, wave optics effects will be even more important. The precise mass scale also depends on the lensing configuration, such as the distance from the caustic, where wave optics effects can become more prominent close to a caustic when the magnification is large.

Figure 2.

Different models of the source plane optical depth to gravitational lensing agree within a factor $\simeq 2$. This indicates that the integral of the optical depth across the mass function of lenses is converged. As discussed in the text, the distribution of the optical depth across the mass function is less well converged and is a key area for theoretical and observational progress. Figure reproduced from [13].

Figure 3.

The peak of the redshift (left) and magnification (right) distributions of detectable lensed sources, as a function of redshift horizon, $z_{\mathrm{H}}$, based on the model and assumptions described in §4a. The comoving rate density evolution of the ‘evolving’ population tracks the SFRD history of the Universe, as described in the text. In the evolving (more commonly used for forecasting) scenario, $z_{\mathrm{H}}\simeq 0.5$ is the approximate transition from detectable lensed sources being dominated by high-magnification lensing ($\mu \gtrsim 10$) to being dominated by low-magnification lensing ($\mu \lesssim 10$).

Figure 4.

Left: The predicted relative rates of discovery of gravitationally lensed GW sources from a number of detailed studies (data points) overlaid on curves based on the multi-messenger model discussed in §4a. The upper (solid) and lower (dashed) curves bracket the range of threshold gravitational magnifications above which galaxy-scale lenses and all lenses (i.e. including massive galaxy clusters) are efficient at forming multiple images. The curves assume $\mathcal{K}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$, as is relevant to GW detectors. Right: The typical redshift horizons out to which different EM sources can be detected without assistance from gravitational magnification ($z_{\mathrm{H}}$, points), shown at an arbitrary offset above the curves, for clarity. The curves assume $\mathcal{K}\propto (1+z)$ for simplicity, i.e. the $k$-correction relevant to an EM source that has a flat $S_{\nu }$ spectrum and detected photometrically. The difference between solid and dashed curves is the same as in the left panel. The expected relative rate of detection of gravitationally lensed images by the respective surveys can be read off from curves at the redshifts that correspond to each of the points.

Figure 5.

GW signals from gravitationally lensed BBHs during the fifth LVK run (as inferred in low latency, assuming $\mu =1$) are predicted to overlap in mass with the bulk of the GW signals—compare red dashed contours with the detections from the first three runs. In contrast, GW signals from gravitationally lensed BNSs are predicted to be dominated by sources that appear in low latency to be located in the so-called ‘mass gap’ between neutron stars and stellar remnant BHs. This allows a more efficient selection of candidate-lensed BNS using magnification-based methods than for candidate-lensed BBHs. This figure is based on work published in [13,119].

Figure 6.

This figure is adapted from the figure available at https://emfollow.docs.ligo.org/userguide/capabilities.html, based on [232]. It shows the predicted cumulative distributions of sky localization uncertainties of GW detections by LVK through to their fifth run. Independent of run or source type, ≃10% of detections will be localized to better than Ω ≃100 degree2 precision. Improvements on this await the extension of the GW detector network, via LIGO India [233]. We also note that in the case where several lensed images are detected, major improvements in the sky localization uncertainties are possible [18].

Figure 7.

Magnification-redshift distributions of messengers from gravitationally lensed BNS mergers, based on table 1, equation (4.2) and §4a. Contours enclose approximately 90% of the predicted lensed detections, and the shaded areas extend to approximately 99% to visualize the tails of the respective distributions, as explained in §4c(i).

Figure 8.

Arrival time difference distributions for the five messenger/instrument combinations shown in figure 7, normalized to an Einstein radius of ${\theta }_{\mathrm{E}}=1\mathrm{arcsec}$, based on combining the magnification distributions shown in that figure with equation (3.13), for lens density profiles that are steep (${\eta }_0=-1$), intermediate (${\eta }_0=-0.5$) and flat (${\eta }_0=-1$) at the mid-point between fold image pairs (§3f,g). The grey shaded region in each panel indicates the region in which $\mu <10$, i.e. where lenses with flatter density profiles tend to be less efficient at forming multiple images (§3g). The distributions are all normalized to the same arbitrary peak value. The overlaps of the arrival time distributions shown in this figure reflect the overlapping distributions in figure 7.

Figure 9.

A schematic for the steps to localize a dark-lensed binary merger. (1) Lensed GW images are detected by the ground-based LVK observatories. (2) The sky localizations from the multiple identified images can be analysed jointly to reduce the final sky localization region [15]. (3) The joint sky region can be cross-matched with gravitational lens catalogues from LSST, Euclid and their contemporaries. (Edited from NASA, ESA, Illingworth, Magee, Oesch, Bouwens and HUDF09 team.) (4) The candidate lenses are individually analysed and reconstructed to test their match to the GW images. (Edited from: NASA/ESA/HST.) (5) If a gravitationally lensed galaxy from the EM lens catalogues stands out as a distinctly high-ranked candidate host of the dark-lensed CBC merger, the CBC can then be localized accurately in the source plane.

Figure 10.

(A) A strongly lensed system produces two images of a GW source (lines), separated by an arrival time difference $\mathit{\Delta }t$ (lower inset). (B) Image II encounters a large projected density of objects (dots) within the lens (with finite radius ${10}^{-4}\times$ the Einstein radius of the strong lens). Colour shows the magnification in the lens plane. The main image is shown as a star and microimages appear as crosses. (C) Microlensing produces a distinct modulation in the GW signal.