Furmidge Equation Revisited

Abstract

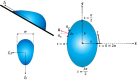
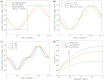
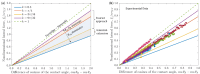
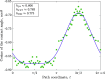
This paper addresses the issue of the discontinuous function that gives rise to the Furmidge equation, a long-standing problem in interfacial science. The force at the contact line of a sliding drop is related to the drop size, the contact angle hysteresis, the surface tension, and a geometrical prefactor k which depends on the distribution of the contact angle about the contact line. The most common expression for the contact line force, called the Furmidge equation, takes k = 1 and is based on a discontinuous contact line, while corrections to this model pose polynomial functional forms for the contact angle, engendering discontinuities in the derivatives. Moreover, experimental findings provide a wide range of k values for different drops on different solids, and this range is yet to be explained in a physical context. Owing to this, the understanding of forces on sliding drops remains lacking. We construct a general model based on a Fourier series, and we further generalize this model by superposing a series of Gaussian curves on our Fourier series. The result of this model is a range of k values, in accordance to the range of experimental values which appear in the literature. Additionally, we fit our functional form for the contact angle to experimental data and find good agreement, as well as good agreement between k values.

Figure 1

Top-left: schematic of the system where a liquid drop slides down a solid incline. Bottom-left: a force, f_∥ acts against the direction of motion while another force, f_LP, is labeled to act in the direction perpendicular to motion along the plane of the solid. Right: a top view of a drop with an elliptical triple line with semiminor and semimajor axes a,b, respectively. The x̂,ŷ components of the normal direction are shown, as is the sector length. In addition, we show the coordinate system, including the parameter t and its values at the front, back, and sides of the drop.

Figure 2

Contact angle model as assumed by Furmidge and Kawasaki. The model is inherently discontinuous at t = π, 0 ≡ 2π (see Figure 1) and is therefore unphysical as shown.

Figure 3

(a) The distribution of cos θ along the drop perimeter for different models, where for the sake of demonstration we take θ_A = 140°,θ_R = 80°. The inherently discontinuous model as well as linear model are both problematic due to discontinuity and the linear model also has asymmetry. On the other hand, the newly proposed model is both continuously periodic and symmetric, as is shown in the figure. (b) the distribution of cos θ along the drop perimeter for contact angle models corresponding to f_∥,min,f_∥,max,f_∥,mid. We again take θ_A = 140°,θ_R = 80°. The minimum value of k corresponds to an inherent lingering on a value between the two angles, while the maximum value corresponds to a lingering on the two extreme values. (c) the variation of cos θ for different values of δ as presented in eq 16 compared to the base case of the Fourier model. We again take θ_A = 140°,θ_R = 80° as described above. We notice a gradual smoothing of the function between the limiting cases of δ → 0 and δ → ∞. Minimal and maximal Fourier cases of the Gaussian model are presented in Section S7 of the Supporting Information. (d) values of k plotted against δ ϵ (0.5,2.5). We see that a value of k = 0.5 is indeed reached, despite the previous findings of the Fourier series without the Gaussian extension.

Figure 4

(a) nondimensional lateral parallel force, f_∥/wγ_LV, plotted against cos θ_R – cos θ_A for all physical models described up until now. The total range of k being between 0.5 and 0.9 is illustrated, and internal ranges are shown and described in terms of the effects of θ_eq against θ_A,θ_R as well as the mathematical modeling. We also include a dashed line representing the Furmidge-Kawasaki model, which is out of range. (b) comparison to experimental data from,^,,,, where data from are adapted from ACS Publishing (Copyright 2022 ACS Publishing), and data from^,,, are adapted with permission from Elsevier (Copyright 1962 Elsevier Publishing, Copyright 1990 Elsevier Publishing, Copyright 1995 Elsevier Publishing, Copyright 2008 Elsevier Publishing).

Figure 5

Fitting the Fourier model (with b₀,a₁,b₂,a₃ nonzero) with data adapted from (Copyright 2022 ACS Publishing). We observe good agreement between the fit and the data, as well as between the k values obtained (both by direct fitting and FFT) to the k value obtained in the reference.