Evolution into chaos - Implications of the trade-off between transmissibility and immune evasion
- PMID: 40322073
- PMCID: PMC12049990
- DOI: 10.1016/j.idm.2025.04.003
Evolution into chaos - Implications of the trade-off between transmissibility and immune evasion
Abstract
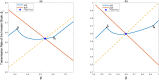
Predicting viral evolution presents a significant challenge and is a critical public health priority. In response to this challenge, we develop a novel model for viral evolution that considers a trade-off between immunity evasion and transmissibility. The model selects for a new strain with the highest invasion fitness, taking into account this trade-off. When the dominant strain of the pathogen is highly transmissible, evolution tends to favor immune evasion, whereas for less contagious strains the direction of evolution leads toward increasing transmissibility. Assuming a linear functional form of this trade-off, we can express the long-term evolutionary patterns following the emergence of subsequent strains by a non-linear difference equation. We provide sufficient criteria for when evolution converges, and successive strains exhibit similar transmissibility. We also identify scenarios characterized by a two-periodic pattern in upcoming strains, indicating a situation where a highly transmissible but not immune-evasive strain is replaced by a less transmissible but highly immune-evasive strain, and vice versa, creating a cyclic pattern. Finally, we show that under certain conditions, viral evolution becomes chaotic and thus future transmissibilites become unpredictable in the long run. Visualization via bifurcation diagrams elucidates our analytical findings, revealing complex dynamic behaviors that include the presence of multiple periodic solutions and extend to chaotic regimes. Our analysis provides valuable insights into the complexities of viral evolution in the light of the trade-off between immune evasion and transmissibility.
Keywords: Chaos; Global stability; Immune evasion; Periodic solutions; Trade-off; Transmissiblity; Viral evolution.
© 2025 The Authors.
Conflict of interest statement
On behalf of all authors of the manuscript entitled 'Evolution into chaos – implications of the trade-off between transmissibility and immune evasion', I confirm that there are no conflicts of interest to declare regarding the publication of this manuscript.
Figures




Similar articles
-
Immune Escape Associated with RBD Omicron Mutations and SARS-CoV-2 Evolution Dynamics.Viruses. 2022 Jul 22;14(8):1603. doi: 10.3390/v14081603. Viruses. 2022. PMID: 35893668 Free PMC article. Review.
-
Modeling the trade-off between transmissibility and contact in infectious disease dynamics.Math Biosci. 2016 Jul;277:15-24. doi: 10.1016/j.mbs.2016.03.010. Epub 2016 Apr 19. Math Biosci. 2016. PMID: 27102055
-
Within-host parasite dynamics, emerging trade-off, and evolution of virulence with immune system.Evolution. 2003 Jul;57(7):1489-97. doi: 10.1111/j.0014-3820.2003.tb00357.x. Evolution. 2003. PMID: 12940354
-
Life-history trade-offs and the evolution of pathogen resistance: competition between host strains.Proc Biol Sci. 1994 Sep 22;257(1350):247-53. doi: 10.1098/rspb.1994.0122. Proc Biol Sci. 1994. PMID: 7991634
-
Strain wars and the evolution of opportunistic pathogens.Curr Opin Microbiol. 2022 Jun;67:102138. doi: 10.1016/j.mib.2022.01.009. Epub 2022 Feb 12. Curr Opin Microbiol. 2022. PMID: 35168173 Review.
References
-
- Allen L. 2007. An introduction to mathematical biology.
-
- Anderson R.M., May R.M. Population biology of infectious diseases: Part i. Nature. 1979;280(5721):361–367. - PubMed
LinkOut - more resources
Full Text Sources

