Benchmarking Quantum Gates and Circuits

Abstract

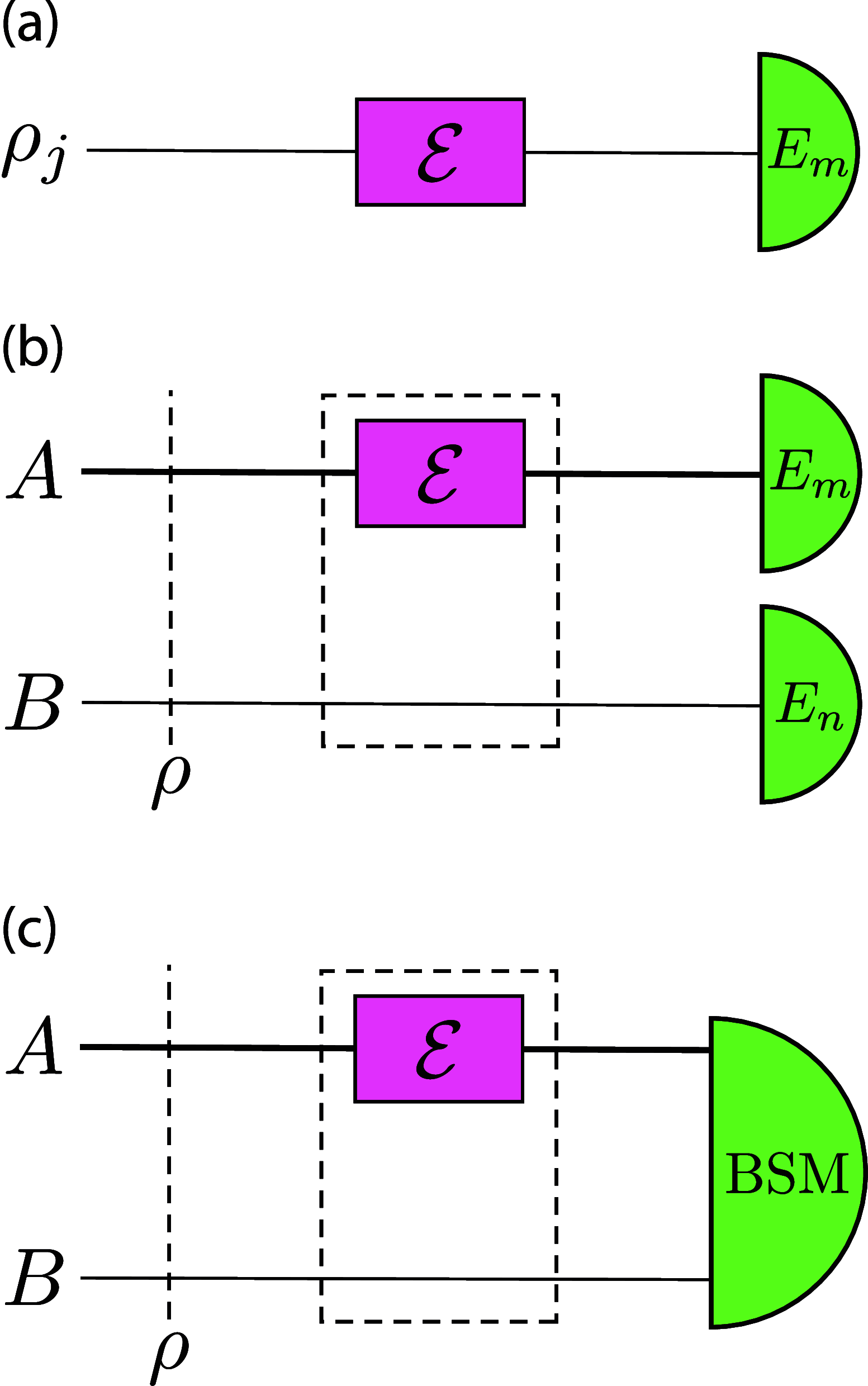
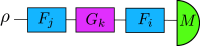
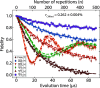
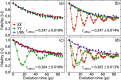
Accurate noise characterization in quantum gates and circuits is vital for the development of reliable quantum simulations for chemically relevant systems and fault-tolerant quantum computing. This paper reviews a variety of key benchmarking techniques, including Randomized Benchmarking, Quantum Process Tomography, Gate Set Tomography, Process Fidelity Estimation, Direct Fidelity Estimation, and Cross-Entropy Benchmarking. We evaluate each method's complexities, the resources they require, and their effectiveness in addressing coherent, incoherent, and state preparation and measurement (SPAM) errors. Furthermore, we introduce Deterministic Benchmarking (DB), a novel protocol that minimizes the number of experimental runs, exhibits resilience to SPAM errors, and effectively characterizes both coherent and incoherent errors. The implementation of DB is experimentally validated using a superconducting transmon qubit, and the results are substantiated with a simple analytical model and master equation simulations. With the addition of DB to the toolkit of available benchmarking methods, this article serves as a practical guide for choosing and applying benchmarking protocols to advance quantum computing technologies.

1

Three different QPT methods. (a) Schematic of SQPT. An ensemble of states {ρ _j } is prepared and each state is subjected to the map $\mathcal{E}$ followed by measurements {E _m }. (b) Schematic of separable AAPT. A “faithful” input state ρ is subjected to the map $\mathcal{E}\otimes I$ . The operators {E _j } are measured on the joint system, which results in the required joint probability distributions or expectation values. (c) Schematic of DCQD. The system and the ancilla are prepared in one of the input states as in Table and are subjected to the map $\mathcal{E}\otimes I$ . The joint system is measured in the Bell-state basis (Bell State Measurement).

2

Gate set tomography circuit consisting of the fiducial gates F _i (F _j ) as well as the measurement operators M and the native gate G _k performed on the initial state ρ. Figure adapted from ref . Copyright 2021 Quantum.

3

Schematic of DFE: To estimate the state fidelity, expectations of random Pauli strings P _j are calculated for the input state ρ. The distribution of the random Pauli strings depends on the state with respect to which the fidelity is being calculated.

4

RCS benchmarking circuit: layers of 2-qubit gates (white boxes) are interleaved with Haar random 1-qubit gates (blue boxes), followed by measurement in the computational basis at the end. Adapted from Figure of ref . Copyright 2021 arXiv.

5

Schematic representations of the gate sequences for (a) randomized benchmarking (RB) and (b) deterministic benchmarking (DB), respectively. RB uses N random Clifford gates C _i , followed by a single recovery gate C _r = C _N ^†···C ₁ ^†. DB prepares an initial state via U|0⟩, applies n repetitions of a fixed, deterministic two-pulse sequence P ₁ P ₂, and unprepares the initial state via U ^†.

6

Empirical (F̃, symbols), analytical fit (F, solid curves), and Lindblad-based (F̅, dashed curves) fidelities for the initial states |1⟩ under free evolution and |+⟩ under various gate sequences P ₁ P ₂. The analytical fit yields T ₁ = 23.36 ± 0.40 μs, T ₂ = 44.13 ± 2.49 μs, δθ = 0.398 ± 0.004°, and δϕ = 0.426 ± 0.004°. With the exception of the XX (orange) and YY (green) cases, the Lindblad-based results are indistinguishable from the analytical fits.

7

Randomized benchmarking measurement for the same gate calibration parameters used in Figure . The error bars represent the deviation of the averaged benchmarking results across 30 distinct random sequences with a maximum number of Cliffords (N _Cliffords) of 700, which are smaller than the marker sizes.

8

Experimental fidelities F̃ ^|+⟩ showing the very different sensitivity of DB and RB to coherent errors. (a) δθ = 0°, δϕ = 0°, (b) δθ = 0°, δϕ = 0.893 ± 0.002°, (c) δθ = 0.932 ± 0.007°, δϕ = 0°, (d) δθ = 0.995 ± 0.009°, δϕ = 0.90 ± 0.002°. These angles are obtained from fits using eq . Dashed curves are the numerically computed fidelities F ^|+⟩ from the open system Lindblad model using the DB parameters above along with the corresponding T ₁ and T ₂. The UR6 sequence suppresses even large coherent errors.

9

Asymmetry in the decay pattern of DB sequences due to the interplay of gates and T ₁. Fidelity decay for (a) XX and (b) YY applied to two pairs of orthogonal initial states. Dashed curves represent the Lindblad master equation simulation results with parameters obtained by fitting eq .

10

Simulated survival fidelity of the |+⟩ state after repetitions of the XX sequence, where each gate is a cosine pulse length of 20 ns (blue circles) or 10 ns (orange squares). A third state in the simulation represents leakage, with a detuning (anharmonicity) of −150 MHz relative to the qubit transition. Both the amplitude and frequency of oscillations increase as the gate duration is decreased and leakage becomes more significant.