Wetting Ridge Growth Dynamics on Textured Lubricant-Infused Surfaces

Abstract

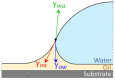
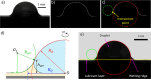
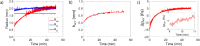
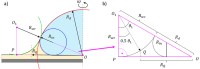
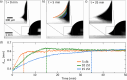
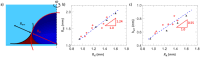
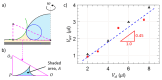
Understanding droplet-surface interactions has broad implications in microfluidics and lab-on-a-chip devices. In contrast to droplets on conventional textured air-filled superhydrophobic surfaces, water droplets on state-of-the-art lubricant-infused surfaces are accompanied by an axisymmetric annular wetting ridge, the source and nature of which are not clearly established to date. Generally, the imbalance of interfacial forces at the contact line is believed to play a pivotal role in accumulating the lubricant oil near the droplet base to form the axisymmetric wetting ridge. In this study, we experimentally characterize and model the wetting ridge that plays a crucial role in droplet mobility. We developed a geometry-based analytical model of the steady-state wetting ridge shape that is validated by using experiments and numerical simulations. Our wetting ridge model shows that at steady state (1) the radius of the wetting ridge is ≈30% higher than the droplet radius, (2) the wetting ridge rises halfway to the droplet radius, (3) the volume of the wetting ridge is half (≈50%) of the droplet volume, and (4) the wetting ridge shape does not depend on the oil viscosity used for impregnation. The insights gained from this work improve our state-of-the-art mechanistic understanding of the wetting ridge dynamics.

Keywords: contact line pinning; fluid-structure interactions; lubricant depletion; lubricant-infused surfaces; three-phase contact line; wetting ridge; wrapping layer.

1

Schematic wetting ridge. Force balance at the contact line where the lubricant oil, water, and air meet determines whether the lubricant oil wraps around the droplet. Owing to the concave inward meniscus shape of the oil–air interface, the region near the droplet base is at lower pressure than the ambient pressure. This low-pressure region siphons oil radially inward from the surrounding oil-infused textured surface. The accumulation of oil near the droplet base gives rise to a skirt-like annular wetting ridge. Depending on oil availability, the wetting ridge can grow and become comparable with the droplet volume.

2

Test sample fabrication protocol. a) A microscope glass slide was coated with hydrophobic colloidal nanoparticles. b) The nano-colloid coated glass slide was over lubricated with silicone oil. c) The glass slide was firmly secured on a spin coater by pulling vacuum. The rotational speed and duration were varied to achieve the desired lubricant film thickness. d) The excess oil on the textured glass slide was thrown out from the surface due to centrifugal force during spin coating. Capillarity force is attributed to immobilizing the lubricant film on the nano-textured glass slide.

3

Wetting ridge. a) Image of a water droplet residing on a textured surface infused with silicone oil (10 cSt at 20 °C) a few seconds after deposition (scale bar = 1 mm). b) Camera image converted to binary using edge detection in Matlab. c) Droplet and wetting ridge fitted with circles. d) Schematic of the water droplet (center “O”) on the lubricant-infused surface. The respective droplet radius, wetting ridge radius (center “O ₁”), and droplet base radius are denoted as R _d, R _wr, and R _Q while the height of the wetting ridge is denoted as h _wr. e) The droplet image after being processed for curve fitting using a custom Matlab script.

4

Wetting ridge growth rate. a) Growth rate of the three radii (R _d, R _Q, and R _wr). The droplet radius R _d is nearly constant while the wetting ridge R _wr and droplet base radius R _Q converge toward each other with time. Droplet radius (R _d) is maintained nearly constant by enclosing the droplet in an optically transparent glass cuvette that suppresses diffusion-driven droplet evaporation. b) Wetting ridge height (h _wr) as a function of time obtained from analyzing time-lapse images. c) Pressure deficit of the wetting ridge (Δp _wr), which is given by subtracting ambient pressure (p _amb) from the wetting ridge pressure (p _wr) using Δp _wr = p _wr - p _amb. Negative pressure indicates pressure below ambient. The inset shows the pressure measurement from meniscus curvature 9 min after deposition with a 95% confidence interval.

5

Wetting ridge model. a) Schematic of a water droplet residing on a textured lubricant-infused surface. The droplet and wetting ridge radii are represented by R _d and R _wr, respectively. A smaller circle with a radius R _in is used to accurately capture the shape of the droplet near its base. b) Geometrical representation of the right angle that forms by connecting the center of the droplet (O), center of the wetting ridge (O ₁), and merging point of the wetting ridge with the lubricant film (P). The line connecting O and O ₁ passes through the intersection of the wetting ridge with the droplet, which is used to define the wetting ridge height. This geometrical depiction is developed to capture the steady-state wetting ridge shape.

6

Effect of oil viscosity on wetting ridge growth dynamics. a–c) Sequential images of wetting ridge growth for a water droplet (≈10 μl) on a textured lubricant-infused surface with varying oil viscosity. The wetting ridge growth rate reaches a steady-state after 35 min for all viscosities. As can be seen from the curve fitting, the wetting ridge grows faster for the low-viscosity oil 5 cSt (orange), followed by 10 cSt (green) and 15 cSt (blue). d) Height of the wetting ridge as a function of time. The wetting ridge grows relatively faster initially for all viscosities. Following initial deposition, the wetting ridge growth rate levels off after 5, 15, and 35 min for 5, 10, and 15 cSt oils, respectively. The final steady-state wetting ridge height for all viscosities nearly is the same at ≈0.6 mm. The time to reach steady-state wetting ridge scales inversely with oil viscosity. The uncertainty in our measurement from repeated experiments for one standard deviation is ≈100 μm.

7

Model validation using Surface Evolver (SE) simulation. a) In the SE numerical simulation, the height of the wetting ridge (h _wr) is determined by identifying the intersection point between the wetting ridge and the water droplet. b) Wetting ridge radius (R _wr) as a function of the droplet radius (R _d). c) Wetting ridge height (h _wr) as a function of the droplet radius. The red circles are experimental data while the black triangles are obtained from SE simulation. This result shows that R _wr = 1.24R _d and h _wr = 0.55R _d, a result that agrees well with our analytical model that gives R _wr = 1.30R _d and h _wr = 0.56R _d. The measurement uncertainty from repeated experiments for one standard deviation is ≈100 μm. The error bars are smaller than the data points.

8

Wetting ridge volume. a) Schematic of the droplet and wetting ridge. b) Cross sectional area of the wetting ridge near the droplet base. The wetting ridge is represented by the blue hatched region. c) Volume of the wetting ridge as a function of the droplet volume. The wetting ridge volume is obtained by rotating the cross sectional area A (blue hatched area) along the axis of the droplet. The red hollow circles are experimental data points while the black hollow triangles are Surface Evolver simulation results. At steady-state, the wetting ridge volume is ≈50% of the droplet volume. The measurement uncertainty is <0.1 μl. The error bars are smaller than the data points.