Macroecological patterns in experimental microbial communities
- PMID: 40341906
- PMCID: PMC12112161
- DOI: 10.1371/journal.pcbi.1013044
Macroecological patterns in experimental microbial communities
Abstract
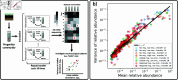
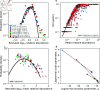
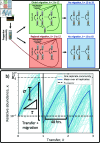
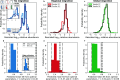
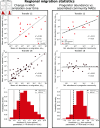
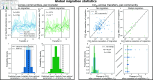
Ecology has historically benefited from the characterization of statistical patterns of biodiversity within and across communities, an approach known as macroecology. Within microbial ecology, macroecological approaches have identified universal patterns of diversity and abundance that can be captured by effective models. Experimentation has simultaneously played a crucial role, as the advent of high-replication community time-series has allowed researchers to investigate underlying ecological forces. However, there remains a gap between experiments performed in the laboratory and macroecological patterns documented in natural systems, as we do not know whether these patterns can be recapitulated in the lab and whether experimental manipulations produce macroecological effects. This work aims at bridging the gap between experimental ecology and macroecology. Using high-replication time-series, we demonstrate that microbial macroecological patterns observed in nature exist in a laboratory setting, despite controlled conditions, and can be unified under the Stochastic Logistic Model of growth (SLM). We found that demographic manipulations (e.g., migration) impact observed macroecological patterns. By modifying the SLM to incorporate said manipulations alongside experimental details (e.g., sampling), we obtain predictions that are consistent with macroecological outcomes. By combining high-replication experiments with ecological models, microbial macroecology can be viewed as a predictive discipline.
Copyright: © 2025 Shoemaker et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

Similar articles
-
Investigating macroecological patterns in coarse-grained microbial communities using the stochastic logistic model of growth.Elife. 2024 Jan 22;12:RP89650. doi: 10.7554/eLife.89650. Elife. 2024. PMID: 38251984 Free PMC article.
-
Metacommunity-scale biodiversity regulation and the self-organised emergence of macroecological patterns.Ecol Lett. 2019 Sep;22(9):1428-1438. doi: 10.1111/ele.13294. Epub 2019 Jun 27. Ecol Lett. 2019. PMID: 31243848
-
Macroecological laws describe variation and diversity in microbial communities.Nat Commun. 2020 Sep 21;11(1):4743. doi: 10.1038/s41467-020-18529-y. Nat Commun. 2020. PMID: 32958773 Free PMC article.
-
The microbial contribution to macroecology.Front Microbiol. 2014 May 5;5:203. doi: 10.3389/fmicb.2014.00203. eCollection 2014. Front Microbiol. 2014. PMID: 24829564 Free PMC article. Review.
-
The macroecological contribution to global change solutions.Science. 2007 Jun 15;316(5831):1581-4. doi: 10.1126/science.1133267. Science. 2007. PMID: 17569854 Review.
References
-
- Brown J. Macroecology. University of Chicago Press. 1995.
-
- Azaele S, Suweis S, Grilli J, Volkov I, Banavar JR, Maritan A. Statistical mechanics of ecological systems: Neutral theory and beyond. Rev Mod Phys. 2016;88(3). doi: 10.1103/revmodphys.88.035003 - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

