Photon-photon chemical thermodynamics of frequency conversion processes in highly multimode systems

Abstract

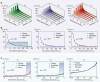
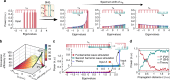
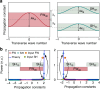
Frequency generation in highly multimode nonlinear optical systems is inherently a complex process, giving rise to an exceedingly convoluted landscape of evolution dynamics. While predicting and controlling the global conversion efficiencies in such nonlinear environments has long been considered impossible, here, we formally address this challenge even in scenarios involving a very large number of spatial modes. By utilizing fundamental notions from optical statistical mechanics, we develop a universal theoretical framework that effectively treats all frequency components as chemical reactants/products, capable of undergoing optical thermodynamic reactions facilitated by a variety of multi-wave mixing effects. These photon-photon reactions are governed by conservation laws that directly determine the optical temperatures and chemical potentials of the ensued chemical equilibria for each frequency species. In this context, we develop a comprehensive stoichiometric model and formally derive an expression that relates the chemical potentials to the optical stoichiometric coefficients, in a manner akin to atomic/molecular chemical reactions. This advancement unlocks new predictive capabilities that can facilitate the optimization of frequency generation in highly multimode photonic arrangements, surpassing the limitations of conventional schemes that rely exclusively on nonlinear optical dynamics. Notably, we identify a universal regime of Rayleigh-Jeans thermalization where an optical reaction at near-zero optical temperatures can promote the complete and entropically irreversible conversion of light to the fundamental mode at a target frequency. Our theoretical results are corroborated by numerical simulations in settings where second-harmonic generation, sum-frequency generation and four-wave mixing processes can manifest.

Fig. 1

Frequency conversion thermodynamic processes in continuous and discrete photonic arrangements. a Schematic of a degenerate four wave-mixing process $2{\omega }_A\rightleftharpoons {\omega }_B+{\omega }_C$, in a ${\chi }^{\left(3\right)}$ graded-index (GRIN) multimode silica fiber. Here, the stoichiometry is mathematically analogous to the reversible reaction of hydrogen iodide $2\mathrm{HI}\rightleftharpoons {\mathrm{H}}_2+{\mathrm{I}}_2$. b Sum-frequency generation process ${\omega }_A+{\omega }_B\rightleftharpoons {\omega }_C$ in a ${\chi }^{\left(2\right)}$ LiNbO₃ nonlinear waveguide lattice, which is conceptually resembling for example thermal decomposition of calcium carbonate, i.e., ${\mathrm{CaCO}}_3\rightleftharpoons \mathrm{CaO}+\mathrm{C}{\mathrm{O}}_2$

Fig. 2

Thermalization dynamics of frequency conversion processes in continuous and discrete photonic arrangements. a Evolution of the average transverse modal occupancies $⟨J_i⟩$ for the three frequency components interacting via degenerate four-wave mixing in the GRIN fiber (Fig. 1a). Here, the fiber core radius is 31.25 µm, with a refractive index contrast of $\left(n_{\mathit{core}}-n_{\mathit{clad}}\right)/n_{\mathit{core}}=0.01$. The core refractive index $n_{\mathit{core}}$ is calculated using the Sellmeier equation for silica. The system is initiated by exciting equally a subset of transverse modes, primarily at frequency ${\omega }_A$. b Comparison between simulation results and theoretical predictions. The resulting RJ equilibria exhibit a common temperature $T=0.25$ and distinct chemical potentials, ${\mu }_A=0.22$, ${\mu }_B=-0.11$, and ${\mu }_C=0.56$, in accord with Eq. (5). c Average modal distributions at thermal equilibrium for a LiNbO₃ lattice configuration involving 30 waveguide elements as depicted in Fig. 1b. The corresponding theoretical temperature and chemical potentials are predicted to be $T=-0.01$ and ${\mu }_A=2.23$, ${\mu }_B=1.42$, and ${\mu }_C=3.65$, resulting in RJ equilibria that match perfectly with numerical simulation results. Here, a negative temperature indicates that higher-order modes are favored

Fig. 3

Optimizing frequency conversion for second-harmonic generation. a Thermal equilibrium states of a SHG optical reaction occurring in a LiNbO₃ lattice involving ten waveguide elements. For all three cases, the system is excited with the same power, shared between the six lower order modes (left panel). As the phase mismatch between the fundamental and harmonic wave increases, the system transits from a positive temperature to a negative temperature regime, where the higher order modes are preferentially populated. The equilibrium power ratios between the SH and FW ($P_B/P_A$) are 0.44, 1.25, 0.7 for the three cases respectively. b Theoretically obtained conversion efficiency as a function of input energy $U$ and phase mismatch $\mathrm{\Delta }$ for a LiNbO₃ lattice involving 30 elements. c Numerically simulated equilibrium power distributions at the maximum conversion efficiency point, marked by the green dot in b. The first two modes of the FW are evenly excited with a total power of $P_A=1.5$ while the two frequencies exhibit a phase mismatch of $\mathrm{\Delta }=2.1$. At thermal equilibrium, the system reaches a near-zero temperature RJ state, with a theoretically predicted $T=0.0018$, matching simulations results. d Optical power evolution as obtained from numerical simulations for the latter case. After thermalization, a conversion efficiency of 91% is attained, in agreement with theoretical predictions

Fig. 4

Optimizing frequency conversion for sum-frequency generation. a Conversion efficiency of the SFG process as a function of input power ratio and phase mismatch $\Delta$, for a LiNbO₃ waveguide array involving 30 waveguide elements. The input energy is set at the optimal zero-temperature value of $U=-P_A{ϵ}_{A,\max }-P_B{ϵ}_{B,\max }$. b Average modal occupancies at equilibrium, obtained via numerical simulation of Eq. (2) at the maximum conversion efficiency point, indicated with a black dot in (a). The two reactants ${\omega }_A$ and ${\omega }_B$ are initially excited with equal powers ($P_A=P_B=1$), each equally distributed in their respective two lower-order modes. In this case, the system thermalizes to a near-zero temperature state with $T=0.0013$, transferring power to the third frequency ${\omega }_C$. c Evolution of the optical power for the optical reactants (${\omega }_A$ or ${\omega }_B$) and products (${\omega }_C$) as obtained from numerical simulations. After thermalization, a conversion efficiency of 92.3% is achieved, consistent with theoretical predictions

Fig. 5

Second-harmonic generation when two mode bands are involved at the second harmonic. a Eigenvalue bands corresponding to the FW (left panel) and the SH (right panel) waves. Note that ${\kappa }_{A,B,C}$ denote the coupling coefficients associated with the local modes for the FW and SH waves, while ${\Delta }_1,{\Delta }_2$ represent the phase mismatch between the FW and SH₀₂, SH₁₀ eigenvalue band. b By judiciously varying either the initial FW excitation conditions or the detuning parameters, the majority of the FW optical power can be funneled towards either the SH₀₂ band (left panel) or the SH₁₀ band (right panel). In all instances, the numerical simulations show excellent agreement with the theoretical predictions