Mathematical Modeling of Influenza Dynamics: Integrating Seasonality and Gradual Waning Immunity

Abstract

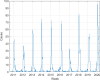
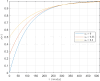
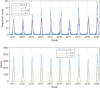
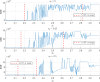
The dynamics of influenza virus spread is one of the most complex to model due to two crucial factors involved: seasonality and immunity. These factors have been typically addressed separately in mathematical modeling in epidemiology. In this paper, we present a mathematical modeling approach to consider simultaneously both forced-seasonality and gradual waning immunity. A seasonal SIRn model that integrates seasonality and gradual waning immunity is constructed. Seasonality has been modeled classically, by defining the transmission rate as a periodic function, with higher values in winter seasons. The progressive decline of immunity after infection has been introduced into the model structure by considering multiple recovered subpopulations or recovery states with transmission rates attenuated by a susceptibility factor that varies with the age of infection. To show the applicability of the proposed mathematical modeling approach to a real-world scenario, we have carried out a calibration of the model with the data series of influenza infections reported in the 2010-2020 period at the General Hospital of Castellón de la Plana, Spain. The results of the case study show the feasibility of the mathematical approach. We provide a discussion of the main features and insights of the proposed mathematical modeling approach presented in this study.

Keywords: Gradual waning immunity; Influenza; Mathematical modeling; Seasonality; Susceptibility.

Fig. 1

Model flow chart of the seasonal SIRn influenza epidemic model

Fig. 2

Seasonal influenza data series: weekly influenza urgent reported cases in the Castellón de la Plana General Hospital in the 2010-2020 period. Source: Clinical Documentation and Admissions Department of the Castellón de la Plana General Hospital (private data)

Fig. 3

Susceptibility functions $s_i(\tau )$ for different initial susceptibility degrees $s_0$ and exponential parameter a

Fig. 4

Best SIRn model solution. Best fit between the SIRn model reported infected and data series (top) and model simulation of total infected I(t) (bottom), for different susceptibility scenarios

Fig. 5

SSE error function for different ${\beta }_0$ parameter values and different susceptibility scenarios. The red dashed lines delimit the ${\beta }_0$ range that satisfies the 5-15% infected per season restriction

Fig. 6

Unrealistic solutions for different susceptibility scenarios. The solutions shown are the 5% of the numerical simulations with the highest SSE