Verhulst-type equation and the universal pattern for global population growth
- PMID: 40388550
- PMCID: PMC12088597
- DOI: 10.1371/journal.pone.0323165
Verhulst-type equation and the universal pattern for global population growth
Abstract
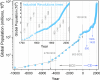
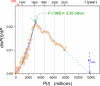
The global population [Formula: see text] (growth from 10,000 BCE to 2023) is discussed in frames of the Verhulst-type scaling, recalling the sustainable development concept. The analysis focuses on the per capita global population growth rate, for which the analytic counterpart is considered:[Formula: see text]. The focused insight reveals two near- linear domains for [Formula: see text] changes: from ~ 700 CE till ~1968 and from ~1968 till 2023. It can be considered a reference pattern for long-term global population changes. For models recalling the Verhulst-type scaling, such analysis indicates that a single pair of growth rate and system resource coefficients [Formula: see text] should describe the rise in the global population. However, the Verhulst relation with such effective parameters does not describe [Formula: see text] changes, which raises the question of whether it is adequate to describe global population changes. Notably is the new way of data preparation, based on their collections from various sources and numerical filtering to obtain a 'smooth' optimal set. The changes of [Formula: see text] were analyzed via the 'reversed protocol' analysis, in comparison to the standard pattern, namely: (i) first, the linearized, distortions-sensitive transformation of [Formula: see text] data is carried out; it indicates domains where the validated application of a given scaling equation is possible and yields optimal values of relevant parameters, (ii) the final fitting via the selected scaling equation is carried out for identified domains, and using obtained optimal values of parameters. The analysis reveals links between [Formula: see text] local 'disturbations' and some historical and prehistorical reference events, showing their global scale impacts.
Copyright: © 2025 Sojecka, Drozd-Rzoska. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
No competing inererests between authors.
Figures


Similar articles
-
An Extension of Janmahasatian's Fat-Free Mass Model for Universal Application Across Populations of Different Ethnicities.Clin Pharmacokinet. 2020 Sep;59(9):1161-1170. doi: 10.1007/s40262-020-00883-1. Clin Pharmacokinet. 2020. PMID: 32201910
-
Fundamental insights into ontogenetic growth from theory and fish.Proc Natl Acad Sci U S A. 2015 Nov 10;112(45):13934-9. doi: 10.1073/pnas.1518823112. Epub 2015 Oct 27. Proc Natl Acad Sci U S A. 2015. PMID: 26508641 Free PMC article.
-
The cooperative free volume rate model for segmental dynamics: Application to glass-forming liquids and connections with the density scaling approach⋆.Eur Phys J E Soft Matter. 2019 Aug 12;42(8):100. doi: 10.1140/epje/i2019-11862-3. Eur Phys J E Soft Matter. 2019. PMID: 31396721
-
Optimal Therapy Scheduling Based on a Pair of Collaterally Sensitive Drugs.Bull Math Biol. 2018 Jul;80(7):1776-1809. doi: 10.1007/s11538-018-0434-2. Epub 2018 May 7. Bull Math Biol. 2018. PMID: 29736596
-
Application of artificial neural networks and multiple linear regression on local bond stress equation of UHPC and reinforcing steel bars.Sci Rep. 2021 Jul 23;11(1):15061. doi: 10.1038/s41598-021-94480-2. Sci Rep. 2021. PMID: 34302020 Free PMC article.
References
-
- Roberts N. The Holocene: An Environmental History. Wiley-Blackwell; New York. 2014. ISBN: 978-1405155212.
-
- Laublicher L. 8 billion humans: population growth, climate change and the ‘Anthropocene engine’. Science. The Wire. 2022:11;11. available at: https://science.thewire.in/environment/population-growth-climate-change-...
-
- Huxley A. Brave New World. Penguin Random House; London: 2004. ISBN: 978-0099477464.
MeSH terms
LinkOut - more resources
Full Text Sources

