Methods in quantitative biology-from analysis of single-cell microscopy images to inference of predictive models for stochastic gene expression
- PMID: 40388970
- PMCID: PMC12150428
- DOI: 10.1088/1478-3975/adda85
Methods in quantitative biology-from analysis of single-cell microscopy images to inference of predictive models for stochastic gene expression
Abstract
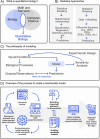
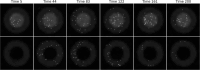
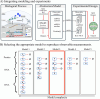
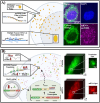
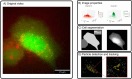
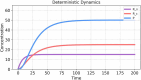
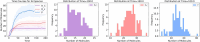
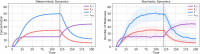
The field of quantitative biology (q-bio) seeks to provide precise and testable explanations for observed biological phenomena by applying mathematical and computational methods. The central goals of q-bio are to (1) systematically propose quantitative hypotheses in the form of mathematical models, (2) demonstrate that these models faithfully capture a specific essence of a biological process, and (3) correctly forecast the dynamics of the process in new, and previously untested circumstances. Achieving these goals depends on accurate analysis and incorporating informative experimental data to constrain the set of potential mathematical representations. In this introductory tutorial, we provide an overview of the state of the field and introduce some of the computational methods most commonly used in q-bio. In particular, we examine experimental techniques in single-cell imaging, computational tools to process images and extract quantitative data, various mechanistic modeling approaches used to reproduce these quantitative data, and techniques for data-driven model inference and model-driven experiment design. All topics are presented in the context of additional online resources, including open-source Python notebooks and open-ended practice problems that comprise the technical content of the annual Undergraduate Quantitative Biology Summer School (UQ-Bio).
Keywords: fluorescence microscopy; mechanistic models; model inference; quantitative biology; single-cell imaging; stochastic gene expression.
Creative Commons Attribution license.
Figures


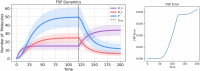
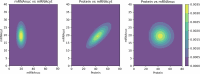
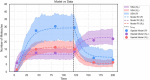
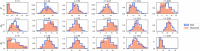
References
-
- Peccoud J, Ycart B. Markovian modeling of gene-product synthesis. Theor. Popul. Biol. 1995;48:222–34. doi: 10.1006/tpbi.1995.1027. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
