Moiré cavity quantum electrodynamics

Abstract

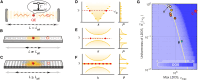
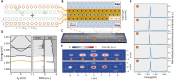
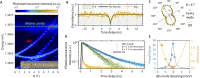
Quantum emitters are a key component in photonic quantum technologies. Enhancing single-photon emission by engineering their photonic environment is essential for improving overall efficiency in quantum information processing. However, this enhancement is often limited by the need for ultraprecise emitter placement within conventional photonic cavities. Inspired by the fascinating physics of moiré pattern, we propose a multilayer moiré photonic crystal with a robust isolated flatband. Theoretical analysis reveals that, with nearly infinite photonic density of states, the moiré cavity simultaneously has a high Purcell factor and large tolerance over the emitter's position, breaking the constraints of conventional cavities. We then experimentally demonstrate various cavity quantum electrodynamic phenomena with a quantum dot in moiré cavity. A large tuning range (up to 40-fold) of quantum dot's radiative lifetime is achieved through strong Purcell enhancement and inhibition effects. Our findings open the door for moiré flatband cavity-enhanced quantum light sources and quantum nodes for the quantum internet.

Fig. 1.. Schematics of photon emission in various photonic structures.

A quantum emitter (QE) marked by a red filled circle respectively placed in (A) a traditional Fabry-Pérot cavity, (B) a 1D defect PhC cavity, and (C) a moiré PhC cavity. Red dashed circles stand for quantum emitters positioned at nonoptimal sites. Black dashed double arrows represent the effective length of cavities with strong LDOS, while gray double arrows denote the full lengths of photonic structures. A quantum emitter is a quantum system with two energy levels: a ground state and an excited state, as illustrated in the inset of (A). When the quantum system transitions from the excited state to the ground state, it emits a single photon with a spontaneous emission rate $\mathrm{\Gamma }$. Left and right panels of (D) to (F) represent the dispersion relations and DOS $P\left(\mathrm{\omega }\right)$ of photonic structures in (A) to (C), respectively. Red dots denote the effective modes in (A) to (C), and red dashed lines mark the transition frequency of the quantum emitter ${\mathrm{\omega }}_0$. In the right panel of (E), the DOS inside the defect PhC cavity and in the bandgap PhC regime are denoted by solid yellow curves. (G) Schematically shows the uniformity of LDOS [${\overline{K}}_{\mathrm{\rho }}=3-\text{Kurt}\mathrm{\rho }({\mathrm{\omega }}_0,x)$] versus the maximum value of LDOS [${\mathrm{\rho }}_{\mathrm{m}}\left({\mathrm{\omega }}_0\right)$] for different fixed DOSs. Circles and squares represent the numerical results of the L3, L5, L7, L10, L15, and L20 and H1 defect PhC cavities, respectively, from top to bottom. Here, we use the L20 cavity as an analogy to the traditional Fabry-Pérot cavity in (A). The orange star represents the moiré PhC cavity. See numerical details in the Supplementary Materials.

Fig. 2.. Design and characterization of moiré flatband cavity.

(A) Two unit cells (gray dashed rectangles) of 1D moiré PhC composed of two 1D PhCs (brown and blue circles) with slightly different lattice constants ($a_1=209.1$ nm, $a_2=194.1$ nm). Other structural parameters: d = 133 nm, s = 95 nm, and L = 2718 nm. (B) SEM image of a fabricated triple-layer moiré PhC unit cell formed by combining two unit cells shown in (A). (C) SEM image of a moiré PhC consisting of five unit cells (white dashed rectangles). (D) Right: Comparison of calculated and experimentally measured photon DOS. The latter is obtained by spatially integrating PL spectra within a moiré PhC unit cell. The orange color indicates the flatband mode. a.u., arbitrary units. (E) Field spatial distribution of moiré flatband modes. Top: Numerical calculation accounting for the spatial resolution of the subsequent optical measurement. Bottom: PL map acquired by scanning the excitation and collection spots over the moiré PhC and recording the maximal PL intensity within 1.3939 to 1.3978 eV. The full width at half maximum (FWHM) of the excitation/collection spot is ~1.5 μm. (F) PL spectra of moiré cavity mode measured at centers of five moiré PhC unit cells marked in (C) under high-power above-barrier excitation. All experiments in this study are performed at T = 3.6 K. The Q factor of moiré cavity modes 1 to 5 are 3309, 3412, 5026, 3134, and 2602, respectively.

Fig. 3.. Manipulation of single-photon emission from a QD in moiré flatband cavity.

(A) Magnetic field–dependent PL spectra of a QD and moiré cavity mode. The QD emission is split into two branches in an external magnetic field applied parallel to the QD growth axis (Faraday geometry). The higher-energy branch is tuned to be resonant with the moiré cavity mode at B = 7 T. The inset depicts a moiré cavity composed of five superlattice periods, with a trapezoid dot marking the QD position. White arrows indicate the horizontal (H) and vertical (V) polarization directions. (B) Second-order correlation measurement of single-photon emission from the QD under p-shell excitation. The black curve is obtained after deconvolving the detection response function from the green fit, yielding a single-photon purity of 0.93 ± 0.09. The uncertainties correspond to one SD from the fit. (C) Polarization of the emission from the QD (brown) and moiré cavity mode (green) characterized at B = 6 T. The polarization of both the QD and moiré cavity mode are dominantly along the longitudinal direction denoted as H in Fig. 1A (inset). (D) Time-resolved PL (TRPL) of the QD measured using an SNSPD. Gray, instrument response function (IRF) with an FWHM of 71 ± 1 ps; blue (orange), single QD detuned (resonant) with moiré cavity mode under LA phonon–assisted excitation; green, QD ensemble in bulk under above-bandgap excitation; black curves, single exponential fit. (E) QD-cavity detuning dependence of Purcell factor and QD lifetime. Solid lines, Lorentzian fit with a fixed FWHM. Error bars represent the uncertainty extracted from exponential fitting.