A Two-State Random Walk Model of Sperm Search on Confined Domains

Abstract

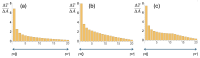
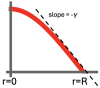
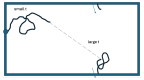
Mammalian fertilization depends on sperm successfully navigating a spatially and chemically complex microenvironment in the female reproductive tract. This process is often conceptualized as a competitive race, but is better understood as a collective random search. Sperm within an ejaculate exhibit a diverse distribution of motility patterns, with some moving in relatively straight lines and others following tightly turning trajectories. Here, we present a two-state random walk model in which sperm switch from high-persistence-length to low-persistence-length motility modes. In reproductive biology, such a switch is often recognized as "hyperactivation". We study a circularly symmetric setup with sperm emerging at the center and searching a finite-area disk. We explore the implications of switching on search efficiency. The first proposed model describes an adaptive search strategy in which sperm achieve improved spatial coverage without cell-to-cell or environment-to-cell communication. The second model that we study adds a small amount of environment-to-cell communication. The models resemble macroscopic search-and-rescue tactics, but without organization or networked communication. Our findings provide a quantitative framework linking sperm motility patterns to efficient search strategies, offering insights into sperm physiology and the stochastic search dynamics of self-propelled particles.

Keywords: persistence length; search trajectories; sperm cell motion.

Figure 1

Representative video microscopy trajectories for approximately 20 human sperm over the course of 26 s in a 563 × 563 μm² field of view at 5× magnification at the objective under negative phase contrast. Following 30 min liquefaction at 37 °C in a 5% CO₂ incubator, sperm were isolated by differential centrifugation in 50% isotonic Percoll. Sperm were resuspended in Biggers, Whitten, and Wiggingham media [15], imaged in a 20 μm deep chambered slide, and temperature was maintained during imaging with a Peltier-heated stage at 37 °C. The sperm cells were observed to move at roughly the same speed, but the persistence lengths differed widely. It is for distinguishability that trajectories have been given different colors.

Figure 2

(a) The searching particle appears in the center of the unit disk and follows Equation (1) with $v_0=1$ and $D_{\theta }=2.0$. The timestep is $\Delta t=0.001$, and the edge of the disk is an absorbing boundary. (b) Initially, the angular diffusion coefficient is $D_{\theta ,1}=0.67$. There is a transition rate $k=2.0$ to switch to $D_{\theta ,2}=6.0$. The part of the trajectory before the switch is almost ballistic and is shown in red. The remaining part is shown in blue. With $k=2.0$ as the transition rate, the switch will, on average, occur close to $r=0.5$. All numerical work in this article was carried out using the Mathematica 13.3 software package.

Figure 3

(a) Trajectories as in Figure 2a were generated, and for each region (one small circle and nineteen annuli), the time spent per unit area, $\Delta T/\Delta A$, was recorded. This figure depicts the averages over 5000 trajectories. (b) As for Figure 2b, we implemented a varying $D_{\theta }$: the searcher leaves the origin with a constant transition rate to the larger value of $D_{\theta }$. This leads to an improved search in that $\Delta T/\Delta A$ becomes larger and more constant. (c) This figure shows how further improvement is achieved upon giving the searcher the ability to “read” its position and let the irreversible transition to the larger $D_{\theta }$ occur when $r=1/2$ is first traversed. Details are in the text.

Figure 4

To the best of our knowledge, Equation (5) has no analytic solution on a disk with an initial condition $P(r,t=0)=\delta \left(r\right)/\left(2\pi r\right)$ and an absorbing boundary at a finite $r=R$. The absorbing boundary implies $P(R,t)=0$ at all times for the evolving $P(r,t)$. We have ${\partial }_{r}P(R,t)=-\gamma$ for the slope at $r=R$. We take this as a first approximation also near the rim. This implies $J(R,t)=D\gamma$ for the amount of probability that crosses the circumference of the disk per unit of time and per unit of distance. With $P(r,t)=\gamma (R-r)$ near $r=R$, we find $v(r,t)=J(r,t)/P(r,t)=D/(R-r)$ for the drift speed toward the rim. Note that this result is independent of $\gamma$. The drift speed $v\left(r\right)=D/(R-r)$ will thus remain at the same value during the entire relaxation.

Figure 5

Equations (3) and (5) are only valid if ${\mathsf{\ell }}_{\mathrm{p}}\to 0$, i.e., if $D_{\theta }$ is very large. We simulate as in Figure 2 and Figure 3, but with $D_{\theta }=200$, leading to ${\mathsf{\ell }}_{\mathrm{p}}=0.005$. The figure on the left is the ensuing bar chart (cf. Figure 3). The figure on the right is a close-up view of the last four bars of the bar chart, together with the best linear fit. The slope of the fit is in good agreement with the prediction of Equation (7).

Figure 6

It is in the cylindrical oviduct that a sperm cell searches for the egg. This search can be modeled as a random walk that starts on the left and has an absorbing boundary on the right. The vertical coordinate is periodic. The geometry is a bit more complicated than this, as the oviduct’s surface has many twists and folds. Nonetheless, it makes sense for the searchers to first rapidly disperse and later switch to a smaller persistence length for a more detailed search.