Observing anyonization of bosons in a quantum gas
- PMID: 40425811
- PMCID: PMC12137132
- DOI: 10.1038/s41586-025-09016-9
Observing anyonization of bosons in a quantum gas
Abstract
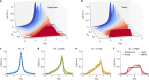
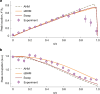
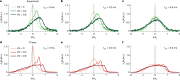
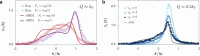
Anyons1,2 are low-dimensional quasiparticles that obey fractional statistics, hence interpolating between bosons and fermions. In two dimensions, they exist as elementary excitations of fractional quantum Hall states3-5 and are believed to enable topological quantum computing6,7. One-dimensional anyons have been theoretically proposed, but their experimental realization has proven to be difficult. Here we observed emergent anyonic correlations in a one-dimensional strongly interacting quantum gas, resulting from the phenomenon of spin-charge separation8-10. A mobile impurity provides the necessary spin degree of freedom to engineer anyonic correlations in the charge sector and simultaneously acts as a probe to reveal these correlations. Starting with bosons, we tune the statistical phase to transmute bosons through anyons to fermions and observe an asymmetric momentum distribution11-14, a hallmark of anyonic correlations. Going beyond equilibrium conditions, we observed dynamical fermionization of the anyons15. This study opens the door to the exploration of non-equilibrium anyonic phenomena in a highly controllable setting15-17.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures

Similar articles
-
Signature of anyonic statistics in the integer quantum Hall regime.Nat Commun. 2024 Aug 3;15(1):6578. doi: 10.1038/s41467-024-50820-0. Nat Commun. 2024. PMID: 39097568 Free PMC article.
-
Demonstrating anyonic fractional statistics with a six-qubit quantum simulator.Phys Rev Lett. 2009 Jan 23;102(3):030502. doi: 10.1103/PhysRevLett.102.030502. Epub 2009 Jan 21. Phys Rev Lett. 2009. PMID: 19257336
-
Realization of one-dimensional anyons with arbitrary statistical phase.Science. 2024 Nov 29;386(6725):1055-1060. doi: 10.1126/science.adi3252. Epub 2024 Nov 28. Science. 2024. PMID: 39607918
-
Charge-neutral electronic excitations in quantum insulators.Nature. 2024 Nov;635(8038):301-310. doi: 10.1038/s41586-024-08091-8. Epub 2024 Nov 13. Nature. 2024. PMID: 39537889 Review.
-
Fractional charge and fractional statistics in the quantum Hall effects.Rep Prog Phys. 2021 Jun 22;84(7). doi: 10.1088/1361-6633/ac03aa. Rep Prog Phys. 2021. PMID: 34015771 Review.
References
-
- Leinaas, J. M. & Myrheim, J. On the theory of identical particles. Il Nuovo Cimento B (1971–1996)37, 1–23 (1977).
-
- Wilczek, F. Quantum mechanics of fractional-spin particles. Phys. Rev. Lett.49, 957–959 (1982).
-
- Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett.48, 1559–1562 (1982).
-
- Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett.50, 1395–1398 (1983).
-
- Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett.53, 722–723 (1984).
LinkOut - more resources
Full Text Sources

