Formation of spatial vegetation patterns in heterogeneous environments

Abstract

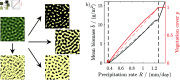
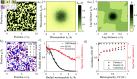
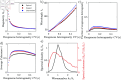
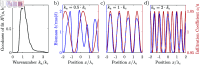
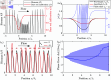
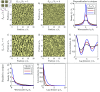
Functioning of many resource-limited ecosystems is facilitated through spatial patterns. Patterns can indicate ecosystems productivity and resilience, but the interpretation of a pattern requires good understanding of its structure and underlying biophysical processes. Regular patterns are understood to form autogenously through self-organization, for which exogenous heterogeneities are negligible. This has been corroborated by reaction-diffusion models which generate highly regular patterns in idealized homogeneous environments. However, such model-generated patterns are considerably more regular than natural patterns, which indicates that the concept of autogenous pattern formation is incomplete. Models can generate patterns which appear more natural when they incorporate exogenous random spatial heterogeneities (noise), such as microtopography or spatially varying soil properties. However, the mechanism through which noise influences the pattern formation has not been explained so far. Recalling that irregular patterns can form through stochastic processes, we propose that regular patterns can form through stochastic processes as well, where spatial noise is filtered through scale-dependent biophysical feedbacks. First, we demonstrate that the pattern formation in nonlinear reaction-diffusion models is highly sensitive to noise. We then propose simple stochastic processes which can explain why and how random exogenous heterogeneity influences the formation of regular and irregular patterns. Finally, we derive linear filters which reproduce the spatial structure and visual appearance of natural patterns well. Our work contributes to a more holistic understanding of spatial pattern formation in self-organizing ecosystems.

Fig 1. Natural vegetation patterns.

(a_i) Irregular vegetation pattern, regularity $S_{rc}/{\lambda }_c$ = 0, p-value of periodicity test 0.97, (a_ii) its periodogram, and (a_iii) its correlogram. Axes normalized by the cut-off wavelength ${\lambda }_l$ = 9 m, beyond which components with shorter wavelength are suppressed. (44^∘10’10"N 5^∘16’22"E, Mt. Ventoux, France). (b_i) Isotropic regular vegetation pattern, regularity $S_{rc}/{\lambda }_c$ = 1.09, p-value of periodicity test 0.98, b_ii) its periodogram and b_iii) its autocorrelation. Axes normalized by the characteristic wavelength ${\lambda }_c=42$ m. (38^∘23’09"N 114^∘52’00"W, Lincoln County, Nevada, USA) (c_i) Anisotropic regular vegetation pattern regularity $S_{x^{+}c}/{\lambda }_c$ = 1.3, $S_{y^{+}c}/{\lambda }_c$ = 3.4, p-value of periodicity test 0.15, (c_ii) its periodogram, and (c_iii) its autocorrelation. Axes normalized by the characteristic wavelength ${\lambda }_c$ = $100$ m. (11^∘10^′18^′′N 28^∘15^′51^′′E, Kordofan, Sudan). Spurious low-frequency components have been suppressed in the periodograms. Images extracted from Google Maps 2023 Maxar Technologies imagery, and were processed in greyscale and thresholded for display. Patterns taken from the dataset of [34]. Note that throughout this manuscript, we use the terms “periodogram” and “correlogram” to the frequency spectrum and sample autocorrelation of an individual pattern, while we use the terms “spectral density” and “autocorrelation” for the frequency spectrum and autocorrelation of the underlying system or model.

Fig 2. Formation of an isotropic regular pattern by a stochastic process which filters a random spatial heterogeneity.

In the real domain, the random heterogeneity e is filtered by convolving $⊛$ it with the impulse response $ℐℛ$ of the filter. Filtering amplifies spatial components of the exogenous heterogeneity close to the characteristic length scale where the autocorrelation function has its fist maximum and attenuates spatial components with shorter or longer wavelength. In the frequency domain, the Fourier transform $ℱ(e)$ of the random heterogeneity is filtered by multiplying it element-wise $\odot$ with the transfer function T of the filter, filtering amplifies frequency components of the noise close to the characteristic frequency where the spectral density $𝒮=|𝒯{|}^2$ is large, and attenuates components with higher or lower frequency.

Fig 3. Thresholding of filter-generated pattern.

(a) A generic isotropic pattern generated by a band-pass filter and a gapped, a labyrinthine and a spotted pattern obtained by thresholding the generic pattern so the vegetation cover is 80%, 50% and 20%, respectively, as well as a ringed pattern obtained by thresholding with a lower and upper level. (b) Relation between biomass and vegetation cover with precipitation in the Rietkerk model. Dashed lines indicate linear approximations.

Fig 4. Spatial heterogeneity of the infiltration coefficient a with mean a¯ and relative standard deviation cv(a) at a unit grid cell size, (a) spatial map, (b) radial spectral density, (c) statistical distribution of the coefficients for three different degrees of heterogeneity cv(a).

Fig 5. Generic irregular patterns.

(a_i) Irregular pattern generated with the grazing model [8, 68] (carrying capacity K with mean ${\mu }_K=8$, spatial coefficient of variation $\text{cv}(K)$ = 0.1 and correlation length ${\theta }_K$ = 1 m, maximum grazing rate $c$ = 2, diffusion $d$ = 0.1, initial homogeneous biomass density b₀ =  2.4724). Axes are normalized with the cut-off wavelength length ${\lambda }_l$. (b) periodogram and (c) correlogram of the pattern generated with the grazing model, Axes normalized with the cut-off length l and corresponding wavenumber k_l = 2 $\pi /{\lambda }_l$. (d) Overlap of the same pattern generated with the grazing model (GM) and with a low-pass filter (LP) from the same spatial map of the parameter K. Both patterns were thresholded for the comparison. The patches largely overlap and with most differences being located at patch fringes. (e) estimated radial density, fitted low-pass density and spectral coherence. (f) Average spectral coherence, goodness of fit of the low-pass generated patterns and of their spectral density with respect to that of the pattern generated by the grazing model, depending on the degree of spatial heterogeneity $cv(K)$.

Fig 6. Regular isotropic patterns generated with the Rietkerk model.

(rainfall intensity R = 0.7 mm/d, runoff velocity $v_x$ = 0, water diffusion $e_x=e_y=100{\text{m}}^2/\text{day}$, spatial extent L² = (1024 m)², spatial resolution $\Delta x$ = 1 m, final time T = 1369 years, random initial condition). Other parameters have the same values as in [17]. (a_i) Highly regular pattern generated in a homogeneous environment ($\mathrm{c}\mathrm{v}(a)$ = 0), regularity $S_{rc}/{\lambda }_c$ = 7.8, p-value of periodicity test 0.00, (b_i) Pattern with intermediate regularity generated in a heterogeneous environment ($\mathrm{c}\mathrm{v}(a)$ = 0.3). regularity $S_{rc}/{\lambda }_c$ = 0.95, p-value of periodicity test 0.63. (a_ii,b_ii) corresponding periodograms, (a_iii,b_iii) corresponding correlogram. The patterns are cropped to an extent of 10 wavelengths for display, approximately one quarter of the model domain.

Fig 7. Response of the Rietkerk model to environmental heterogeneity in flat terrain.

(a) Regularity and (b) wavelength of isotropic patterns generated with the Rietkerk model depending on the degree of exogenous spatial heterogeneity $\text{cv}(a)$ of the infiltration coefficient a. (c) Fraction of the total heterogeneity of infiltration contributed by the exogenous spatial variation of the infiltration coefficient c_a, c.f. Eq 22. (e) Spectral coherence depending on the degree of exogenous spatial heterogeneity. (f) Spectral density of a spotted pattern generated with the Rietkerk model ($\text{cv}(a)$ = 0.1) and spectral coherence with the exogenous spatial heterogeneity.

Fig 8. Frequency response of the Rietkerk model.

(a) Correlation of a one-dimensional pattern generated with the Rietkerk model, where the infiltration coefficient $a$ varies sinusoidally with a varying frequency. The coefficient $a$ varies sinusoidally in space with wavenumber $k_a=2\pi /{\lambda }_a$, a mean $\overline{a}$ of 0.2 mm/d and a relative amplitude of 5%. The correlation is highest, when the coefficient oscillates at a wavelength close to that of the pattern ${\lambda }_a\approx {\lambda }_c$. (b–d) Parts of the pattern generated by varying the infiltration coefficient sinusoidally. In case the wavenumber of the heterogeneity matches that of the pattern, the vegetation stripes align with the infiltration coefficient (d_ii), and the pattern is highly correlated with the infiltration coefficient (a), so that the vegetation pattern is imposed by the exogenous heterogeneity. The vegetation stripes do not align with the infiltration coefficient and the correlation between the pattern and the infiltration coefficient is low when the infiltration coefficient varies at a wavelength considerably smaller (d_i) or larger (d_iii) than the wavelength of the pattern.

Fig 9. Generic isotropic patterns.

(a_i–a_iii) Patterns with several degrees of regularity $S_{rc}/{\lambda }_c$ generated by band-pass filtering a spatially varying heterogeneity and subsequent thresholding. (b) Corresponding radial spectral densities and (c) autocorrelation. The autocorrelation is corrected for the spurious decay introduced by radial averaging. (d) Fit of the bandpass spectral density to the radial density of the natural regular isotropic pattern in Fig 1b_i. (e) Goodness of fit of the bandpass spectral density the radial spectral density of the isotropic regular patterns generated with the Rietkerk model, depending on the degree of exogenous heterogeneity $\text{cv}(a)$. Parameter settings identical to those in Fig. 7. (f) Goodness of fit between patterns generated by bandpass filtering and patterns generated with the Rietkerk model for the same spatial heterogeneity map. (g) Overlap and difference thresholded spotted patterns generated with the Rietkerk model (RK) and generated by band-pass (BP) filtering the spatially infiltration coefficient. The spatial structure of both patterns agrees well ($\text{cv}(a)$ = 0.3).

Fig 10. Anisotropic regular patterns generated with the Rietkerk model (rainfall intensity R = 1 mm/d, runoff velocity vx = 10 m/day, and water diffusion ex = 0, ey=20 m2/day, other parameters are set to the same values specified in

Fig 6). (a_i) A highly regular pattern generated in a homogeneous environment ($\mathrm{c}\mathrm{v}(a)$ = 0), regularity $S_{x^{+}c}/{\lambda }_c$ = 11.6, $S_{y^{+}c}/{\lambda }_c$ = 13.4, p-value of periodicity test = 0.00. (b_i) a less regular pattern with spatially varying infiltration coefficient ($\mathrm{c}\mathrm{v}(a)$ = 0.1), regularity $S_{x^{+}c}/{\lambda }_c$ = 1.52, $S_{y^{+}c}/{\lambda }_c$ = 1.3, p-value of periodicity test = 0.08. (a_ii, b_ii) corresponding periodograms, (a_iii, b_iii) corresponding correlograms.

Fig 11. Response of the Rietkerk model to environmental heterogeneity at hillslopes.

( a) Regularity of anisotropic patterns generated with the Rietkerk model and ( b) the migration celerity of vegetation stripes depending on the degree of random exogenous spatial heterogeneity of the infiltration coefficient $\text{cv}(a)$. Model parameters set to the same values as in Fig 10. The red vertical line in a) indicates the amount of heterogeneity beyond which patterns are not any more periodic at a 0.05 confidence level. ( c) Fit of the noisy oscillator density to the density perpendicular to the stripes of the natural anisotropic pattern in Fig 1c_ii. d) Goodness of fit of the oscillator density to the density perpendicular to the stripes of the anisotropic patterns generated with the Rietkerk model, c.f. Fig 12.

Fig 12. Similarity of striped vegetation patterns with noisy oscillators.

(a_i) Influence of a localized perturbation of the infiltration coefficients on a striped pattern. (a_ii) corresponding local amplitude, phase shift and wavelength. The wavelength and amplitude are locally reduced where the infiltration is inhibited but recover further downhill. In contrast, the phase of the pattern does not recover. Consecutive perturbations in a heterogeneous environment thus accumulate along the pattern and result in a random walk of its phase. (b_i) Influence of a randomly perturbed infiltration coefficient ($\text{cv}(a)$ = 0.1), precipitation R = 1 mm/d, surface water advection $v_x$ = 10 m/d, surface water diffusion e_x = 0. Horizontal bars indicated $\pm 1$ standard deviation of the expected phase deviation. (b_ii) Corresponding phase deviation of the same pattern with respect to a pattern forming in an idealized homogeneous environment. The shaded area indicates the standard deviation of the expected phase deviation, determined from 100 model runs.

Fig 13. Generic anisotropic patterns.

(a–d) Striped patterns generated with the nonlinear oscillator for varying degrees of regularity. (e–f) Corresponding densities S_x and autocorrelation R_x in the direction perpendicular to the stripes. (g–h) Corresponding densities S_y and autocorrelation R_y in the direction parallel to the stripes. The two-dimensional density and autocorrelation are given by the outer product of the one-dimensional densities. The more regular a pattern, the higher the maximum $S_{xyc}\approx S_{x^{+}c}{S}_{y^{+}c}/(4{\lambda }_c^2)$ of the spectral density, and the less rapidly the autocorrelation R_xy = $R_x\otimes R_y$ decays. The regularity of striped patterns can be anisotropic, i.e., it differs between the directions parallel and perpendicular to the stripes. Therefore, two parameters are necessary to unambiguously specify the regularity. This leads to a larger variety of striped patterns compared to isotropic spot and gap patterns, where the regularity is uniquely determined by a single parameter.

Fig 14. Formation of spatial patterns under various conditions:

Patterns forming in homogeneous environments through scale-dependent feedbacks become periodic. Patterns forming in heterogeneous environments through scale-dependent feedbacks become regular, but not periodic. Patterns forming in heterogeneous environments without scale-dependent feedbacks become irregular.