Spontaneous symmetry breaking and panic escape

Abstract

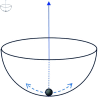
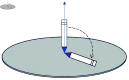
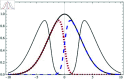
Panic-induced herding in individuals often leads to social disasters, resulting in people being trapped and trampled in crowd stampedes triggered by panic. We introduce a novel approach that offers fresh insights into studying the phenomenon of asymmetrical panic-induced escape. Our approach is based on the concept of Spontaneous Symmetry Breaking (SSB), a fundamental governing mechanism in the Physical Sciences. By applying the principles of SSB, we conjecture that the onset of disastrous effects of panic can be understood as a SSB phenomenon, and we formulate the process accordingly. We highlight that this way of understanding panic escape leads to simple general measures of preventing catastrophic situations, by considering two crucial parameters: population density and external information. The interplay of these two parameters is responsible for either breaking or restoring the symmetry of a system. We describe how these parameters are set by design conditions as well as crowd control. Based on these parameters, we discuss strategies for preventing potential social disasters caused by asymmetrical panic escape.

Fig 1. Ants escaping from a chamber with two exits symmetrically positioned under low and high panic conditions, adapted from Ref [12].

Fig 2. An example of a system with symmetry.

A ball is moving inside a hemispherical bowl. The system is invariant under rotations around the vertical axis. The oscillating motion of the ball on any given vertical plane would transform to a similar oscillating motion but on another vertical plane. However, the state of minimal energy (ball at rest at the bottom of the bowl) is unique and invariant under the symmetry transformation.

Fig 3. An example of SSB.

A pen standing vertically on its tip is unstable: to reach its minimal energy it will fall into a horizontal position, thus pointing into some direction. Although the system has a symmetry around the vertical axis (any direction is equivalent), the state of minimum energy breaks that symmetry.

Fig 4. Cost function V(ϕ) in two scenarios.

Left: symmetric scenario where $\rho <{\rho }_c$ and therefore the minimum of V is at ${\varphi }_0=0$. Right: broken symmetry scenario where $\rho >{\rho }_c$ and therefore ${\varphi }_0\ne 0$. The scales are in arbitrary units.

Fig 5. Example of a symmetric distribution n(x) at t=0 (solid thick black) and at a later time (solid thin black).

The left-mover (red dotted) and right-mover (blue dashed) distributions $n_L^{(0)}(x)$ and $n_R^{(0)}(x)$ are also shown. The normalization and distance units are arbitrary.

Fig 6. Example of a symmetric distribution n(x) at t=0 (solid thick black) which is not symmetric at later times (solid thin black).

The integral of right movers $n_R^{(0)}$ (blue dashed) is larger than the integral of left movers $n_L^{(0)}$ (red dotted). Here we assumed ${\varphi }_0=3$. The normalization and distance units are arbitrary.