Hydration Contribution to the Solvation Free Energy of Water-Soluble Polymers

Abstract

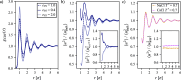
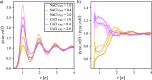
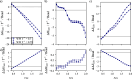
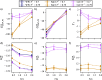
We study the solvation free energy of model water-soluble polymers with an emphasis on better understanding the entropic contribution deriving from the formation of a dynamic hydration layer (DHL). To isolate the solvation free energy due to polymer hydration from contributions that arise from changes in the polymer conformation (and thus solvent-accessible surface area) that ordinarily accompany solvation, we restrict a polymer chain in a rod-like configuration. As in recent works, the nanoscale mobility gradient around the polymer chain, defining the DHL, is quantified through the determination of the Debye-Waller parameter, ⟨u²⟩, for solvent in the vicinity of the polymer. This gradient enables us to easily visualize the DHL around the polymer. Direct computation of the free energy of solvation indicates a large entropic contribution that correlates with changes in Kirkwood-Buff integrals, which allow us to quantify specific ion effects on polymer solvation. While the water mobility exhibits a significant dependence on the strength of the polymer-solvent interaction in the nanoscale DHL, we unexpectedly found no additional specific ion effect on the mobility within the DHL relative to the bulk solution and, moreover, we find no change in the spatial extent of the DHL to within experimental uncertainty. On the other hand, we find an excess density of CsCl close to the polymer and density depletion of NaCl, consistent with previous suggestions that chaotropic ions partition toward polymer interfaces. Our work indicates that polymer hydration can make a large contribution to polymer solvation free energy, and we expect this phenomenon to be important in relation to understanding the thermodynamics of molecular self-assembly and phase separation processes of water-soluble polymers.

1

Simulated system setup in dimensions of 67 σ × 67 σ × 30 σ. A solvated 30-mer polymer is attached to itself through the z-coordinate. A portion of the solvent beads is removed for visualization purposes so that the polymer is clearly shown.

2

(a) Cylindrical distribution function (CDF) of solvent around an infinitely long straight-chain polymer at T* = 0.7 without the presence of salt for variable cross-interaction parameters. (b) Debye–Waller parameter ⟨u ²⟩ at T* = 0.7 without salt and scaled by bulk value with an inlaid plot of these same profiles scaled by the gradient for ϵ_PS = 1. (c) Relative Debye–Waller parameter ⟨u ²⟩ for 1 mol/L NaCl and CsCl solution scaled by their respective bulk values. Inlay represents ⟨u ²⟩ profiles scaled by the no salt solution case. Full-temperature and salt-dependent trends are found in Section S6 of the Supporting Information. Shaded regions represent the standard deviation over the three independent boxes and may be smaller than the plotted trend.

3

(a) Cylindrical distribution function (CDF) of Na⁺ and Cs⁺ around a long rod-like polymer. (b) Difference in CDF between solvent and ions around the polymer; note that a Gaussian filter with a standard deviation of five was applied to improve readability. Uncertainty intervals represent the standard deviation over three independent simulation boxes, where large uncertainties indicate a region with poor sampling of solvent molecules or may be smaller than the plotted trend.

4

For a system without salt, the (a) free energy, (b) enthalpy, and (c) entropy of solvation, i.e., free energy to decouple the polymer and solvent, are plotted with respect to the interaction energy between polymer and solvent for two temperatures. The difference in solvation (d) free energy, (e) enthalpy, and (f) entropy between low and high temperatures illustrate temperature-dependent solvation behavior. Uncertainty intervals may be smaller than data markers, which represent the standard deviation over three independent simulation boxes.

5

Kirkwood–Buff integrals using the CDF between (a) the polymer and ions (both anion and cation), (b) the polymer and solvent, and (c) the interaction parameter of the ions relative to the solvent. These can be compared to Kirkwood–Buff integrals using the SDF between (d) the solvent and solvent, (f) the cation and cation, and (g) the anion and cation. Uncertainty intervals represent the standard deviation over three independent simulation boxes and may be smaller than the data markers.

6

Truncated Kirkwood–Buff integrals at a cutoff. The top row represents values of G _ij at r _cut = 1.68 σ in bulk solution for (a) solvent and solvent, (b) cation and cation, and (c) anion and cation. The inlay of (c) illustrates how the KBI varies between these two solution environments, resulting in the values at the cutoff reported here. The bottom row represents values taken from solution beads in the dynamic hydration layer (DHL) for (d) solvent and solvent, (e) cation and cation, (f) and anion and cation. Uncertainty intervals represent the standard deviation over three independent simulation boxes and may be smaller than data markers.

7

Coordination number (a) around for polymer and solution (including solvent and ions) and (b) between solution and solution. These coordination numbers were taken at the first minimum of the RDF, which was at (1.57 ± 0.01) σ and (1.51 ± 0.01) σ for the two cases, respectively. (c) Coordination number between solution and solution beads in the dynamic hydration layer within 2.5 σ of the polymer. Uncertainty intervals represent the standard deviation over three independent simulation boxes and may be smaller than data markers.