This is a preprint.
Genetic association meta-analysis is susceptible to confounding by between-study cryptic relatedness
- PMID: 40463146
- PMCID: PMC12132175
- DOI: 10.1101/2025.05.10.653279
Genetic association meta-analysis is susceptible to confounding by between-study cryptic relatedness
Abstract
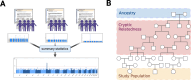
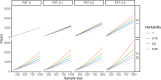
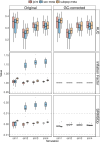
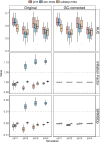
Meta-analysis of Genome-Wide Association Studies (GWAS) has important advantages, but it assumes that studies are independent, which does not hold when there is relatedness between studies. As a motivating example, recent work suggested applying sex-stratified meta-analysis to correct for participation bias, without considering that men and women from the same population will be highly related. Our theory demonstrates how cryptic relatedness results in correlated test statistics between studies, inflating meta-analysis. We characterize the effects of different between-study relatedness scenarios, particularly population structure and recent family relatedness, on meta-analysis type I error control and power. We simulated data with (1) no family relatedness between subpopulations, (2) family relatedness within subpopulations, (3) family relatedness across subpopulations, and (4) single population with family relatedness. We run joint and meta-analyses on simulations using both binary and quantitative traits. In scenarios with family relatedness, sex-stratified meta-analysis exhibits severe inflation and lower AUC compared to joint and subpopulation meta-analyses. Remarkably, genomic control succeeds in correcting inflation in these cases, but does not alter calibrated power. Analysis of real datasets confirms severe inflation for sex-stratified meta-analysis in family studies, but a negligible effect for population studies with up to 10,000 individuals. Our theoretical framework demonstrates that the inflation factor increases as the sample size increases. We recommend against meta-analyzing studies that share the same populations, which increases the risk of inflation due to cryptic relatedness between studies.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures

Similar articles
-
On the impact of relatedness on SNP association analysis.BMC Genet. 2017 Dec 6;18(1):104. doi: 10.1186/s12863-017-0571-x. BMC Genet. 2017. PMID: 29212447 Free PMC article.
-
Correcting for cryptic relatedness in population-based association studies of continuous traits.Hum Hered. 2010;69(1):28-33. doi: 10.1159/000243151. Epub 2009 Oct 2. Hum Hered. 2010. PMID: 19797906 Free PMC article.
-
Confounding from cryptic relatedness in case-control association studies.PLoS Genet. 2005 Sep;1(3):e32. doi: 10.1371/journal.pgen.0010032. PLoS Genet. 2005. PMID: 16151517 Free PMC article.
-
Overview of techniques to account for confounding due to population stratification and cryptic relatedness in genomic data association analyses.Heredity (Edinb). 2011 Apr;106(4):511-9. doi: 10.1038/hdy.2010.91. Epub 2010 Jul 14. Heredity (Edinb). 2011. PMID: 20628415 Free PMC article. Review.
-
Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas.Cochrane Database Syst Rev. 2022 Feb 1;2(2022):CD014217. doi: 10.1002/14651858.CD014217. Cochrane Database Syst Rev. 2022. PMID: 36321557 Free PMC article.
References
Publication types
Grants and funding
- U01 DK085501/DK/NIDDK NIH HHS/United States
- U01 DK085524/DK/NIDDK NIH HHS/United States
- U01 DK085545/DK/NIDDK NIH HHS/United States
- N01 HC065236/HL/NHLBI NIH HHS/United States
- N01 HC065235/HL/NHLBI NIH HHS/United States
- R01 DK047482/DK/NIDDK NIH HHS/United States
- N01 HC065234/HL/NHLBI NIH HHS/United States
- N01 HC065237/HL/NHLBI NIH HHS/United States
- R01 DK053889/DK/NIDDK NIH HHS/United States
- U01 DK057295/DK/NIDDK NIH HHS/United States
- N01 HC065233/HL/NHLBI NIH HHS/United States
- U01 DK085526/DK/NIDDK NIH HHS/United States
- U01 DK085584/DK/NIDDK NIH HHS/United States
LinkOut - more resources
Full Text Sources
Research Materials
