Adolescent maturation of cortical excitation-inhibition ratio based on individualized biophysical network modeling
- PMID: 40465711
- PMCID: PMC12136046
- DOI: 10.1126/sciadv.adr8164
Adolescent maturation of cortical excitation-inhibition ratio based on individualized biophysical network modeling
Abstract
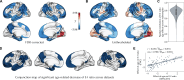
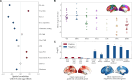
The excitation-inhibition ratio is a key functional property of cortical microcircuits which changes throughout an individual's lifespan. Adolescence is considered a critical period for maturation of excitation-inhibition ratio. This has primarily been observed in animal studies. However, there is limited human in vivo evidence for maturation of excitation-inhibition ratio at the individual level. Here, we developed an individualized in vivo marker of regional excitation-inhibition ratio in human adolescents, estimated using large-scale simulations of biophysical network models fitted to resting-state functional imaging data from both cross-sectional (n = 752) and longitudinal (n = 149) cohorts. In both datasets, we found a widespread decrease in excitation-inhibition ratio in association areas, paralleled by an increase or lack of change in sensorimotor areas. This developmental pattern was aligned with multiscale markers of sensorimotor-association differentiation. Although our main findings were robust across alternative modeling configurations, we observed local variations, highlighting the importance of methodological choices for future studies.
Figures

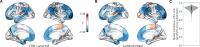
Update of
-
Adolescent maturation of cortical excitation-inhibition balance based on individualized biophysical network modeling.bioRxiv [Preprint]. 2024 Jun 18:2024.06.18.599509. doi: 10.1101/2024.06.18.599509. bioRxiv. 2024. Update in: Sci Adv. 2025 Jun 6;11(23):eadr8164. doi: 10.1126/sciadv.adr8164. PMID: 38948771 Free PMC article. Updated. Preprint.
Similar articles
-
Adolescent maturation of cortical excitation-inhibition balance based on individualized biophysical network modeling.bioRxiv [Preprint]. 2024 Jun 18:2024.06.18.599509. doi: 10.1101/2024.06.18.599509. bioRxiv. 2024. Update in: Sci Adv. 2025 Jun 6;11(23):eadr8164. doi: 10.1126/sciadv.adr8164. PMID: 38948771 Free PMC article. Updated. Preprint.
-
In vivo whole-cortex marker of excitation-inhibition ratio indexes cortical maturation and cognitive ability in youth.Proc Natl Acad Sci U S A. 2024 Jun 4;121(23):e2318641121. doi: 10.1073/pnas.2318641121. Epub 2024 May 30. Proc Natl Acad Sci U S A. 2024. PMID: 38814872 Free PMC article.
-
Key Brain Network Nodes Show Differential Cognitive Relevance and Developmental Trajectories during Childhood and Adolescence.eNeuro. 2018 Jul 11;5(4):ENEURO.0092-18.2018. doi: 10.1523/ENEURO.0092-18.2018. eCollection 2018 Jul-Aug. eNeuro. 2018. PMID: 30073200 Free PMC article.
-
Space-Time Dynamics of Membrane Currents Evolve to Shape Excitation, Spiking, and Inhibition in the Cortex at Small and Large Scales.Neuron. 2017 Jun 7;94(5):934-942. doi: 10.1016/j.neuron.2017.04.038. Neuron. 2017. PMID: 28595049 Review.
-
Interpreting PET and fMRI measures of functional neural activity: the effects of synaptic inhibition on cortical activation in human imaging studies.Brain Res Bull. 2001 Feb;54(3):267-73. doi: 10.1016/s0361-9230(00)00435-4. Brain Res Bull. 2001. PMID: 11287131 Review.
References
-
- Shine J. M., Müller E. J., Munn B., Cabral J., Moran R. J., Breakspear M., Computational models link cellular mechanisms of neuromodulation to large-scale neural dynamics. Nat. Neurosci. 24, 765–776 (2021). - PubMed
-
- Anderson J. S., Carandini M., Ferster D., Orientation tuning of input conductance, excitation, and inhibition in cat primary visual cortex. J. Neurophysiol. 84, 909–926 (2000). - PubMed
-
- Okun M., Lampl I., Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities. Nat. Neurosci. 11, 535–537 (2008). - PubMed
-
- Tan A. Y. Y., Zhang L. I., Merzenich M. M., Schreiner C. E., Tone-evoked excitatory and inhibitory synaptic conductances of primary auditory cortex neurons. J. Neurophysiol. 92, 630–643 (2004). - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

