Visualizing dynamics of charges and strings in (2 + 1)D lattice gauge theories
- PMID: 40468064
- PMCID: PMC12158766
- DOI: 10.1038/s41586-025-08999-9
Visualizing dynamics of charges and strings in (2 + 1)D lattice gauge theories
Abstract
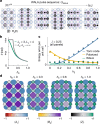
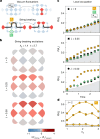
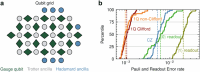
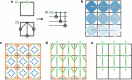
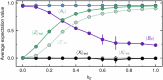
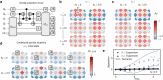
Lattice gauge theories (LGTs)1-4 can be used to understand a wide range of phenomena, from elementary particle scattering in high-energy physics to effective descriptions of many-body interactions in materials5-7. Studying dynamical properties of emergent phases can be challenging, as it requires solving many-body problems that are generally beyond perturbative limits8-10. Here we investigate the dynamics of local excitations in a LGT using a two-dimensional lattice of superconducting qubits. We first construct a simple variational circuit that prepares low-energy states that have a large overlap with the ground state; then we create charge excitations with local gates and simulate their quantum dynamics by means of a discretized time evolution. As the electric field coupling constant is increased, our measurements show signatures of transitioning from deconfined to confined dynamics. For confined excitations, the electric field induces a tension in the string connecting them. Our method allows us to experimentally image string dynamics in a (2+1)D LGT, from which we uncover two distinct regimes inside the confining phase: for weak confinement, the string fluctuates strongly in the transverse direction, whereas for strong confinement, transverse fluctuations are effectively frozen11,12. We also demonstrate a resonance condition at which dynamical string breaking is facilitated. Our LGT implementation on a quantum processor presents a new set of techniques for investigating emergent excitations and string dynamics.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures

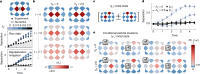
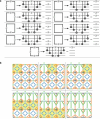
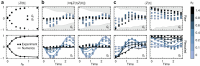
 being excited at time t = 3.5: P(i, j|
being excited at time t = 3.5: P(i, j| ). The different columns correspond to different
). The different columns correspond to different  , indicated by the boxed
, indicated by the boxed  symbols. The unconditioned probability that
symbols. The unconditioned probability that  is excited is written below the
is excited is written below the  symbol. The colour scale represents P(i, j|
symbol. The colour scale represents P(i, j| ) for all i and j. The top and bottom rows show results for hE = 0 and 2.0, respectively. We implement dynamical decoupling and randomized compiling to mitigate control errors, as well as idle dephasing (Methods).
) for all i and j. The top and bottom rows show results for hE = 0 and 2.0, respectively. We implement dynamical decoupling and randomized compiling to mitigate control errors, as well as idle dephasing (Methods).




References
-
- Wegner, F. J. Duality in generalized Ising models and phase transitions without local order parameters. J. Math. Phys.12, 2259–2272 (1971).
-
- Wilson, K. G. Confinement of quarks. Phys. Rev. D10, 2445 (1974).
-
- Kogut, J. & Susskind, L. Hamiltonian formulation of Wilson’s lattice gauge theories. Phys. Rev. D11, 395 (1975).
-
- Kogut, J. B. An introduction to lattice gauge theory and spin systems. Rev. Mod. Phys.51, 659 (1979).
-
- Weinberg, S. The Quantum Theory of Fields (Cambridge Univ. Press, 1995).
LinkOut - more resources
Full Text Sources
Research Materials

