CEST MRI data analysis using Kolmogorov-Arnold network (KAN) and Lorentzian-KAN (LKAN) models

Abstract

Purpose: To investigate the potential of using Kolmogorov-Arnold Network (KAN) and propose Lorentzian-KAN (LKAN) for CEST MRI data analysis (CEST-KAN/CEST-LKAN).

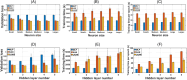
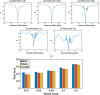
Methods: CEST MRI data acquired from 27 healthy volunteers at 3 T were used in this study. Data from 25 subjects were used for training and validation (548 865 Z-spectra), whereas the remaining two were reserved for testing (51 977 Z-spectra). The performance of multi-layer perceptron (MLP), KAN, and LKAN models was evaluated and compared to conventional multi-pool Lorentzian fitting (MPLF) method in generating ΔB₀, water, and multiple CEST contrasts, including amide, relayed nuclear Overhauser effect (rNOE), and magnetization transfer (MT).

Results: The KAN and LKAN showed higher accuracy in predicting CEST parameters compared to MLP, with average reductions in test loss of 28.37% and 32.17%, respectively. Voxel-wise correlation analysis also revealed that ΔB₀ and four other CEST parameters from the KAN and LKAN had higher average Pearson coefficients than MLP by 1.57% and 2.84%, indicating superior performance. LKAN exhibited a shorter average training time by 37.26% and a smaller average test loss by 5.29% compared to the KAN. Furthermore, our results demonstrated that even smaller KAN and LKAN could achieve better accuracy than MLPs, with both KAN and LKAN showing greater robustness to noisy data compared to MLP.

Conclusion: This study demonstrates the feasibility of KAN and LKAN for CEST MRI data analysis, highlighting their superiority over MLP. The findings suggest that CEST-KAN and CEST-LKAN have the potential to be robust and reliable post-analysis tools for CEST MRI in clinical settings.

Keywords: Kolmogorov‐Arnold network (KAN); Lorentzian‐KAN (LKAN); chemical exchange saturation transfer (CEST); human brain; multi‐pool Lorentzian fitting (MPLF).

FIGURE 1

(A) Illustration of data analysis for CEST MRI using multi‐pool Lorentzian fitting (MPLF), multi‐layer perception (MLP), Kolmogorov‐Arnold network (KAN), and Lorentzian‐KAN (LKAN) methods. The input is the Z‐spectrum, and the output is multiple CEST fitting parameters. (B) Schematic illustration of the activation function of KAN parameterized by B‐splines with grid size = 5. (C) Schematic illustration of the activation function of LKAN parameterized by Lorentzian functions with grid size = 5.

FIGURE 2

Average training and validation results of multi‐layer perceptions (MLPs), Kolmogorov‐Arnold network (KANs), and Lorentzian‐KAN (LKANs) with different neurons size (A–C) and different numbers of hidden layers (D–F). The average results from five trials for each network are presented, with error bars indicating SD. (A) and (D) Validation loss. (B) and (E) Training time. (C) and (F) Training time per epoch.

FIGURE 3

Application of the trained multi‐layer perception (MLP), Kolmogorov‐Arnold network (KAN), and Lorentzian‐KAN (LKAN) to test CEST dataset acquired from two human subjects. Correlation plots of predicted ΔB₀ (ppm) and amplitude values (a.u.) for (A) MLP, (B) KAN, and (C) LKAN versus multi‐pool Lorentzian fitting (MPLF) fitting results (ground truth). R values in plots denote the Pearson correlation coefficient between prediction and ground truth. The columns represent the corresponding ΔB₀, water, amide, relayed nuclear Overhauser effect (rNOE), and magnetization transfer (MT) plots.

FIGURE 4

ΔB₀, Water and CEST amplitude maps of multi‐layer perception (MLP), Kolmogorov‐Arnold network (KAN), and Lorentzian‐KAN (LKAN) applied to the testing data of subject 1 that was not included in training, compared to multi‐pool Lorentzian fitting (MPLF) fitting results. ΔB₀ was measured in ppm and amplitude values were in arbitrary units (a.u.). (A) ΔB₀, water and CEST amplitude maps obtained by MPLF method. (B) ΔB₀, Water and CEST amplitude maps obtained by MLP method. (C) ΔB₀, water and CEST amplitude maps obtained by KAN method. (D) ΔB₀, Water and CEST amplitude maps obtained by LKAN method. (E–G) Absolute difference (|Diff|) maps between the MPLF fitting outcomes and the predictions of the MLP, KAN, and LKAN models, respectively. The rows represent the corresponding ΔB₀, water, amide, relayed nuclear Overhauser effect (rNOE), and magnetization transfer (MT) amplitude maps.

FIGURE 5

Comparison of the Z‐spectra in the testing data of subject 1, reconstructed using the CEST fitting parameters predicted by multi‐pool Lorentzian fitting (MPLF), multi‐layer perception (MLP), Kolmogorov‐Arnold network (KAN), and Lorentzian‐KAN (LKAN). (A) Three regions of interest (ROIs) used for generating the Z‐spectra of white matter (green), gray matter (orange) and cerebrospinal fluid (blue). (B) Comparison of MLP with MPLF. (C) Comparison of KAN with MPLF. (D) Comparison of LKAN with MPLF.

FIGURE 6

Average training results from five trials of multi‐layer perception (MLP), Kolmogorov‐Arnold network (KAN), and Lorentzian‐KAN (LKAN) at different noise levels, with error bars indicating SD. (A–E) Demonstrations of Z‐spectra at the noise levels of 0.01, 0.02, 0.05, 0.1, and 0.2, respectively. (F) Test loss.

FIGURE 7

Global feature importance plot visualizing the top 20 most influential input features (based on the mean absolute Shapley additive explanations [SHAP] values) to the predicted outputs of (A) amplitude value of water, (B) ΔB₀ (ppm), (C) amplitude value of amide (a.u.), (D) amplitude value of relayed nuclear Overhauser effect (rNOE) (a.u.), and (E) amplitude value of magnetization transfer (MT) (a.u.). The rows represent the corresponding multi‐layer perception (MLP), Kolmogorov‐Arnold network (KAN), and Lorentzian‐KAN (LKAN).