Bland-Altman Plot for Censored Variables
- PMID: 40474442
- PMCID: PMC12141777
- DOI: 10.1002/sim.70147
Bland-Altman Plot for Censored Variables
Abstract
The comparison of two measurement methods turns out to be a statistical challenge if some of the observations are below the limit of quantification or detection. Here we show how the Bland-Altman plot can be modified for censored variables. The reference lines (bias and limits of agreement) in the Bland-Altman plot have to be estimated for censored variables. In a simulation study, we compared three different estimation methods: Restricting the data set to fully quantifiable pairs of observations (complete case analysis), naïvely substituting missing values with half of the limit of quantification, and a multiple imputation procedure based on a maximum likelihood approach for bivariate lognormally distributed variables with censoring. The results show that simple ad-hoc solutions may lead to bias in the results when comparing two measurement methods with censored observations, whereas the presented multiple imputation approach of the Bland-Altman method allows adequate consideration of censored variables. The method works similarly for other distribution assumptions.
Keywords: difference plot; limited variable; nondetects.
© 2025 The Author(s). Statistics in Medicine published by John Wiley & Sons Ltd.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures

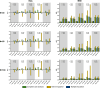
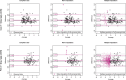

References
-
- Altman D. G. and Bland J. M., “Measurement in Medicine: The Analysis of Method Comparison Studies,” Journal of the Royal Statistical Society Series D (The Statistician) 32, no. 3 (1983): 307–317, 10.2307/2987937. - DOI
-
- Bland J. M. and Altman D. G., “Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement,” Lancet 1, no. 8476 (1986): 307–310. - PubMed
-
- Bland J. M. and Altman D. G., “Agreed Statistics: Measurement Method Comparison,” Anesthesiology 116, no. 1 (2012): 182–185. - PubMed
-
- Lotz A., Tulowietzki J. F., Kendzia B., et al., “Censored Data and Statistics: How to Estimate Percentiles,” in Symposium on Detection Limits in Air Quality and Environmental Measurements (ASTM International, 2019), 161–180.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
