Mathematical proof of the Fisher-Escolà Q statistical distribution in quantum consciousness modeling
- PMID: 40475802
- PMCID: PMC12137171
- DOI: 10.1016/j.csbj.2025.04.025
Mathematical proof of the Fisher-Escolà Q statistical distribution in quantum consciousness modeling
Abstract
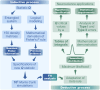
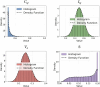
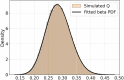
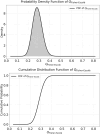
Quantum theories have long sought to explain conscious experience, yet their biggest challenge is not conceptual but methodological. A critical gap remains: the lack of statistical tools capable of empirically testing these theories against objective reality. This study introduces and formalizes the Q of Fisher-Escolà distribution, the first statistical model to integrate quantum and classical probabilities, enabling robust inferential analysis in neuroscience and consciousness studies. We examined 150 density matrices of entangled states in a 10-qubit quantum system using IBM's quantum supercomputers. Through maximum likelihood estimation, we mathematically confirmed that Q Fisher-Escolà ∼ beta(a, b, loc, scale). As a key contribution, a novel analytical solution to the Quantum Fisher Information (QFI) integral was derived, improving decoherence stability. Additionally, 10⁵ Monte Carlo simulations allowed us to establish critical thresholds for α = 0.05, 0.01, 0.001, and 0.0001, while assessing Type I and II error rates. Type I errors appeared in 2-5 % of right-tailed tests at α = 0.05 but approached zero as α decreased. Type II errors occurred in left-tailed tests (1-4 % at α = 0.05) but also diminished with stricter significance levels. In two-tailed tests, both error types remained below 3 %, highlighting the distribution's robustness. The Q of Fisher-Escolà distribution pioneers a statistical framework for modeling quantum-classical interactions in consciousness research. It enables hypothesis testing and predicting subjective experiences, with applications in neuroscience and computational automation. Supported by mathematical proofs and empirical validation, this model advances the integration of quantum probability into neuroscience.
Keywords: Hypothesis testing; Q Fisher-Escolà Distribution; Quantum Fisher Information; Quantum consciousness; Quantum entanglement.
© 2025 The Authors.
Conflict of interest statement
The authors wish to confirm that there are no known conflicts of interest associated with this publication.
Figures


Similar articles
-
Further N-Frame networking dynamics of conscious observer-self agents via a functional contextual interface: predictive coding, double-slit quantum mechanical experiment, and decision-making fallacy modeling as applied to the measurement problem in humans and AI.Front Comput Neurosci. 2025 Apr 1;19:1551960. doi: 10.3389/fncom.2025.1551960. eCollection 2025. Front Comput Neurosci. 2025. PMID: 40235846 Free PMC article.
-
Evidence of quantum-entangled higher states of consciousness.Comput Struct Biotechnol J. 2025 Mar 10;30:21-40. doi: 10.1016/j.csbj.2025.03.001. eCollection 2025. Comput Struct Biotechnol J. 2025. PMID: 40171221 Free PMC article.
-
Quantum Metrology: Surpassing the shot-noise limit with Dzyaloshinskii-Moriya interaction.Sci Rep. 2015 Nov 9;5:16360. doi: 10.1038/srep16360. Sci Rep. 2015. PMID: 26549409 Free PMC article.
-
Quantum Theory of the Classical: Einselection, Envariance, Quantum Darwinism and Extantons.Entropy (Basel). 2022 Oct 24;24(11):1520. doi: 10.3390/e24111520. Entropy (Basel). 2022. PMID: 36359613 Free PMC article. Review.
-
Consciousness, biology and quantum hypotheses.Phys Life Rev. 2012 Sep;9(3):285-94. doi: 10.1016/j.plrev.2012.07.001. Epub 2012 Jul 10. Phys Life Rev. 2012. PMID: 22925839 Review.
References
-
- Aerts D., Sozzo S. Quantum entanglement in concept combinations. Int J Theor Phys. 2013;53(10):3587–3603. doi: 10.1007/s10773-013-1946-z. - DOI
-
- Albarelli F., Gianani I., Genoni M.G., Barbieri M. Fisher-information susceptibility for multiparameter quantum estimation. Phys Rev A. 2024;110(3) doi: 10.1103/physreva.110.032436. - DOI
-
- Bell J.S. On the einstein podolsky rosen paradox. Phys Phys Fiz. 1964;1(3):195–200. doi: 10.1103/physicsphysiquefizika.1.195. - DOI
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous
