Mathematical proof of the Fisher-Escolà Q statistical distribution in quantum consciousness modeling

Abstract

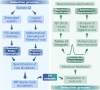
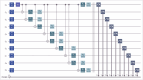
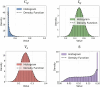
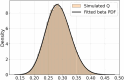
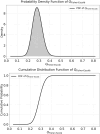
Quantum theories have long sought to explain conscious experience, yet their biggest challenge is not conceptual but methodological. A critical gap remains: the lack of statistical tools capable of empirically testing these theories against objective reality. This study introduces and formalizes the Q of Fisher-Escolà distribution, the first statistical model to integrate quantum and classical probabilities, enabling robust inferential analysis in neuroscience and consciousness studies. We examined 150 density matrices of entangled states in a 10-qubit quantum system using IBM's quantum supercomputers. Through maximum likelihood estimation, we mathematically confirmed that Q _{Fisher-Escolà} ∼ beta(a, b, loc, scale). As a key contribution, a novel analytical solution to the Quantum Fisher Information (QFI) integral was derived, improving decoherence stability. Additionally, 10⁵ Monte Carlo simulations allowed us to establish critical thresholds for α = 0.05, 0.01, 0.001, and 0.0001, while assessing Type I and II error rates. Type I errors appeared in 2-5 % of right-tailed tests at α = 0.05 but approached zero as α decreased. Type II errors occurred in left-tailed tests (1-4 % at α = 0.05) but also diminished with stricter significance levels. In two-tailed tests, both error types remained below 3 %, highlighting the distribution's robustness. The Q of Fisher-Escolà distribution pioneers a statistical framework for modeling quantum-classical interactions in consciousness research. It enables hypothesis testing and predicting subjective experiences, with applications in neuroscience and computational automation. Supported by mathematical proofs and empirical validation, this model advances the integration of quantum probability into neuroscience.

Keywords: Hypothesis testing; Q Fisher-Escolà Distribution; Quantum Fisher Information; Quantum consciousness; Quantum entanglement.

Graphical abstract

Fig. 1

Schematic and logical diagram of Escolà-Gascón's experiment. This experiment investigated the effects of qubit entanglement on the contingency configuration between emotional stimuli and point movement. The movement of the points (RDM stimuli) became uniform (either leftward or rightward) only after each participant’s anticipation. The central question was whether the covert presentation of emotional stimuli could enable participants to perceive or predict, through quantum-like mechanisms, classically unpredictable stimuli associated with point movement.

Fig. 2

Summary of the development steps for theQof Fisher-Escolà distribution. This figure provides a conceptual map of the development process, mathematical formulation, and statistical analyses of the Fisher-Escolà Q distribution, structured into outward (inductive) and return (deductive) logical paths.

Fig. 3

Applied explanation of the Fisher-Escolà paradox. This diagram presents a metaphorical interpretation of the Fisher-Escolà paradox. Classical statistical methods fall short when applied to quantum phenomena, as they fail to capture the subtle microvariations inherent at that level. Rather than forcing classical tools onto quantum systems, the proposed approach seeks a middle ground—combining both ontological levels through quantum circuits that incorporate superposition, entanglement, and minimal decoherence (noise). The fish tank metaphor illustrates this contrast: quantum reality appears opaque to classical analysis, while macroscopic reality tends to obscure quantum effects due to excessive deterministic filtering. The aim is to reshape quantum dynamics in a way that makes its information more accessible. One promising strategy involves integrating quantum Fisher information, making it possible to apply this paradox to physical systems beyond the microscopic scale.

Fig. 4

EM1 Circuit: 10-Qubit System with Successive CNOT Gates. The EM1 circuit consists of 10 qubits with successive CNOT gates that generate non-local correlations, inducing entangled states. The R gates are rotational gates that modulate entanglement levels. Measurements were binary, with one collapse per qubit, ensuring the most precise configuration. However, statistically, longer sequences can be produced, extending beyond the 10-qubit limit. The effectiveness of entanglement effects on collapses depends on the qubit states. By logical deduction, the highest variability in defining the theoretical distribution of Q_{Fisher-Escolà} is achieved when each qubit undergoes exactly one collapse.

Fig. 5

Descriptive Statistics ofMonte CarloSimulations. We conducted 10⁵Monte Carlo simulations using the Kernel Density Estimation (KDE) method to estimate the density functions of the histograms. Below are the descriptive statistics for each distribution: (a) global concurrency: Mean = 0.524373, Standard Deviation = 0.036046, Skewness = 3.176115, and Kurtosis = 15.686106. (b) I_Q: Mean = 0.495488, Standard Deviation = 0.096909, Skewness = -0.004207, and Kurtosis = -0.034250. (c) V_k: Mean = 0.251313, Standard Deviation = 0.035653, Skewness = 0.070194, and Kurtosis = -0.128742. (d) β: Mean = 0.130817, Standard Deviation = 0.053233, Skewness = -0.315361, and Kurtosis = -1.176788. These values provide insight into the distributional properties of the simulated data, highlighting variations in dispersion, asymmetry, and tail behavior.

Fig. 6

Distribution andProbability Density Function(PDF) ofQ_{Fisher-Escolà}. This figure illustrates the Q_{Fisher-Escolà} distribution based on 10⁵Monte Carlo random simulations, derived from the simulated distributions presented in Fig. 5. These simulations correspond to each component of the Q_{Fisher-Escolà} statistic (Eq. (32)).

Fig. 7

TheoreticalQ_{Fisher-Escolà}distribution. The theoretical Q_{Fisher-Escolà} distribution serves as a model for statistical inference on variances that integrate both quantum and classical probabilities. (52), (53) define the mathematical expressions and algorithms underlying these graphs.