Sources of information waste in neuroimaging: mishandling structures, thinking dichotomously, and over-reducing data
- PMID: 40476042
- PMCID: PMC12140072
- DOI: 10.52294/apertureneuro.2022.2.zrji8542
Sources of information waste in neuroimaging: mishandling structures, thinking dichotomously, and over-reducing data
Abstract
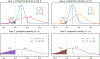
Neuroimaging relies on separate statistical inferences at tens of thousands of spatial locations. Such massively univariate analysis typically requires an adjustment for multiple testing in an attempt to maintain the family-wise error rate at a nominal level of 5%. First, we examine three sources of substantial information loss that are associated with the common practice under the massively univariate framework: (a) the hierarchical data structures (spatial units and trials) are not well maintained in the modeling process; (b) the adjustment for multiple testing leads to an artificial step of strict thresholding; (c) information is excessively reduced during both modeling and result reporting. These sources of information loss have far-reaching impacts on result interpretability as well as reproducibility in neuroimaging. Second, to improve inference efficiency, predictive accuracy, and generalizability, we propose a Bayesian multilevel modeling framework that closely characterizes the data hierarchies across spatial units and experimental trials. Rather than analyzing the data in a way that first creates multiplicity and then resorts to a post hoc solution to address them, we suggest directly incorporating the cross-space information into one single model under the Bayesian framework (so there is no multiplicity issue). Third, regardless of the modeling framework one adopts, we make four actionable suggestions to alleviate information waste and to improve reproducibility: 1) model data hierarchies, 2) quantify effects, 3) abandon strict dichotomization, and 4) report full results. We provide examples for all of these points using both demo and real studies, including the recent Neuroimaging Analysis Replication and Prediction Study (NARPS).
Keywords: Bayesian multilevel modeling; data hierarchy; dichotomization; effect magnitude; information waste; multiple testing problem; result reporting.
Figures


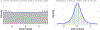



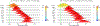

Similar articles
-
Fighting or embracing multiplicity in neuroimaging? neighborhood leverage versus global calibration.Neuroimage. 2020 Feb 1;206:116320. doi: 10.1016/j.neuroimage.2019.116320. Epub 2019 Nov 5. Neuroimage. 2020. PMID: 31698079 Free PMC article.
-
Handling Multiplicity in Neuroimaging Through Bayesian Lenses with Multilevel Modeling.Neuroinformatics. 2019 Oct;17(4):515-545. doi: 10.1007/s12021-018-9409-6. Neuroinformatics. 2019. PMID: 30649677 Free PMC article.
-
Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas.Cochrane Database Syst Rev. 2022 Feb 1;2(2022):CD014217. doi: 10.1002/14651858.CD014217. Cochrane Database Syst Rev. 2022. PMID: 36321557 Free PMC article.
-
Translational Metabolomics of Head Injury: Exploring Dysfunctional Cerebral Metabolism with Ex Vivo NMR Spectroscopy-Based Metabolite Quantification.In: Kobeissy FH, editor. Brain Neurotrauma: Molecular, Neuropsychological, and Rehabilitation Aspects. Boca Raton (FL): CRC Press/Taylor & Francis; 2015. Chapter 25. In: Kobeissy FH, editor. Brain Neurotrauma: Molecular, Neuropsychological, and Rehabilitation Aspects. Boca Raton (FL): CRC Press/Taylor & Francis; 2015. Chapter 25. PMID: 26269925 Free Books & Documents. Review.
-
An integrative Bayesian approach to matrix-based analysis in neuroimaging.Hum Brain Mapp. 2019 Oct 1;40(14):4072-4090. doi: 10.1002/hbm.24686. Epub 2019 Jun 12. Hum Brain Mapp. 2019. PMID: 31188535 Free PMC article.
Cited by
-
Go Figure: Transparency in neuroscience images preserves context and clarifies interpretation.ArXiv [Preprint]. 2025 Apr 10:arXiv:2504.07824v1. ArXiv. 2025. PMID: 40297230 Free PMC article. Preprint.
-
Processing, evaluating, and understanding FMRI data with afni_proc.py.Imaging Neurosci (Camb). 2024 Nov 12;2:1-52. doi: 10.1162/imag_a_00347. eCollection 2024 Nov 1. Imaging Neurosci (Camb). 2024. PMID: 39575179 Free PMC article.
-
Evidence of functional connectivity disruptions between auditory and non-auditory regions in adolescents living with HIV.Front Syst Neurosci. 2025 Jun 5;19:1508516. doi: 10.3389/fnsys.2025.1508516. eCollection 2025. Front Syst Neurosci. 2025. PMID: 40538463 Free PMC article.
-
Which software packages did researchers use to meta-analyze fMRI data? A literature survey from 2019 to 2024.Front Hum Neurosci. 2025 Jul 10;19:1580808. doi: 10.3389/fnhum.2025.1580808. eCollection 2025. Front Hum Neurosci. 2025. PMID: 40708807 Free PMC article.
-
Processing, evaluating and understanding FMRI data with afni_proc.py.ArXiv [Preprint]. 2024 Aug 22:arXiv:2406.05248v3. ArXiv. 2024. Update in: Imaging Neurosci (Camb). 2024 Nov 12;2:1-52. doi: 10.1162/imag_a_00347. PMID: 39398207 Free PMC article. Updated. Preprint.
References
-
- Zhang L, Guindani M, Versace F, Engelmann JM, Vannucci M. A spatiotemporal nonparametric Bayesian model of multi-subject fMRI data. Annals of Applied Statistics. 2016. Jun;10(2):638–66.
-
- Worsley KJ, Evans AC, Marrett S, Neelin P. A Three-Dimensional Statistical Analysis for CBF Activation Studies in Human Brain. Journal of Cerebral Blood Flow & Metabolism. 1992. Nov;12(6):900–18. - PubMed
-
- Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved Assessment of Significant Activation in Functional Magnetic Resonance Imaging (fMRI): Use of a Cluster-Size Threshold. Magnetic Resonance in Medicine. 1995;33(5):636–47. - PubMed
-
- Smith SM, Nichols TE. Threshold-free cluster enhancement: Addressing problems of smoothing, threshold dependence and localisation in cluster inference. NeuroImage. 2009. Jan;44(1):83–98. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
