Prediction of respiratory droplets evolution for safer academic facilities planning amid COVID-19 and future pandemics: A numerical approach

Abstract

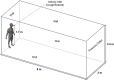
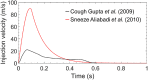
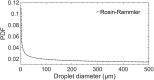
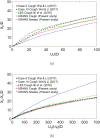
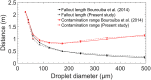
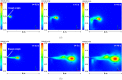
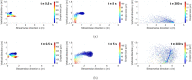
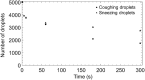
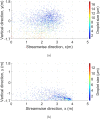
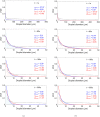
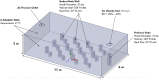
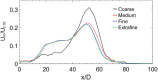
Airborne dispersion of the novel SARS-CoV-2 through the droplets produced during expiratory activities is one of the main transmission mechanisms of this virus from one person to another. Understanding how these droplets spread when infected humans with COVID-19 or other airborne infectious diseases breathe, cough or sneeze is essential for improving prevention strategies in academic facilities. This work aims to assess the transport and fate of droplets in indoor environments using Computational Fluid Dynamics (CFD). This study employs unsteady Reynolds-Averaged Navier-Stokes (URANS) simulations with the Euler-Lagrange approach to visualize the location of thousands of droplets released in a respiratory event and their size evolution. Furthermore, we assess the dispersion of coughing, sneezing, and breathing saliva droplets from an infected source in a classroom with air conditioning and multiple occupants. The results indicate that the suggested social distancing protocol is not enough to avoid the transmission of COVID-19 since small saliva droplets ( ≤ 12 μm) can travel in the streamwise direction up to 4 m when an infected person coughs and more than 7 m when sneezes. These droplets can reach those distances even when there is no airflow from the wind or ventilation systems. The number of airborne droplets in locations close to the respiratory system of a healthy person increases when the relative humidity of the indoor environment is low. This work sets an accurate, rapid, and validated numerical framework reproducible for various indoor environments integrating qualitative and quantitative data analysis of the droplet size evolution of respiratory events for a safer design of physical distancing standards and air cleaning technologies.

Keywords: Airborne transmission; CFD; COVID-19; Indoor environments; Pandemics; Probability density function.

Fig. 1

3D Model Geometry and computational domain.

Fig. 2

Quiescent room mesh.

Fig. 3

Bulk injection velocity profile as function of time for coughing and sneezing.

Fig. 4

Initial droplet distribution.

Fig. 5

Comparison of the maximum streamwise penetration distance as a function of time at (a) starting-jet stage (b) interrupted-jet stage.

Fig. 6

Comparison of the fallout length and contamination range for different droplet sizes.

Fig. 7

Instantaneous velocity contours at 0.5 s, 5 s, and 10 s after a person (a) coughs and (b) sneezes.

Fig. 8

Instantaneous droplet sizes contours at at 0.5 s, 5 s, and 300 s after a person (a) coughs and (b) sneezes.

Fig. 9

Sneezing and coughing droplets lifetime.

Fig. 10

Instantaneous droplet sizes contours at (a) 50% RH and (b) 0% RH at 5 min after coughing.

Fig. 11

(a) Probability density functions for coughing and sneezing at 1 s, 60 s, 180 s and 300 s after an infected person coughs or sneezes. (b) Probability density functions for 50% and 0% RH at 1 s, 60 s, 180 s and 300 s after an infected person coughs.

Fig. 12

Classroom model and boundary conditions.

Fig. 13

Instantaneous droplet sizes contours at at 1 s, 10 s, and 60 s after an infected student seated in the third row of a classroom (a) breaths (b) coughs and (c) sneezes.

Fig. 14

Effect of mesh size on dimensionless cough puff centerline velocity.