Spatial reasoning via recurrent neural dynamics in mouse retrosplenial cortex

Abstract

From visual perception to language, sensory stimuli change their meaning depending on previous experience. Recurrent neural dynamics can interpret stimuli based on externally cued context, but it is unknown whether they can compute and employ internal hypotheses to resolve ambiguities. Here we show that mouse retrosplenial cortex (RSC) can form several hypotheses over time and perform spatial reasoning through recurrent dynamics. In our task, mice navigated using ambiguous landmarks that are identified through their mutual spatial relationship, requiring sequential refinement of hypotheses. Neurons in RSC and in artificial neural networks encoded mixtures of hypotheses, location and sensory information, and were constrained by robust low-dimensional dynamics. RSC encoded hypotheses as locations in activity space with divergent trajectories for identical sensory inputs, enabling their correct interpretation. Our results indicate that interactions between internal hypotheses and external sensory data in recurrent circuits can provide a substrate for complex sequential cognitive reasoning.

Fig. 1. RSC represents spatial information conjunctively with hypothesis states during navigation with locally ambiguous landmarks.

a, Two perceptually identical landmarks are visible only from close up, and their identity is defined only by their relative location. One of 16 ports, at landmark ‘b,’ delivers reward in response to a nose-poke. The animal must infer which of the two landmarks is ‘b’ to receive reward; wrong pokes result in timeout. Tetrode array recordings in RSC yield 50–90 simultaneous neurons. b, Top, schematic example trial; bottom, best possible guesses of the mouse position. LM0, LM1 and LM2 denote task phases when the mouse has seen zero, one or two landmarks and could infer their position with decreasing uncertainty. c, Left, example training curve showing P_hit/P_{false-positive}; random chance level is 1/16 for 16 ports. Mice learned the task at values >1, showing they could disambiguate between the two sequentially visible landmarks. This requires the formation, maintenance and use of spatial hypotheses. Asterisks denote per-session binomial 95% significance for the correct rate. Right, summary statistics show binomial CIs on last half of sessions for all four mice. d, Mouse location heatmap from one session (red) with corresponding spatial firing rate profiles for five example cells; color maps are normalized per cell. e, Task phase (corresponding to hypothesis states in b can be decoded from RSC firing rates. Horizontal line, mean; gray shaded box, 95% CI. f, Spatial coding changes between LM1 and LM2 phases (Euclidean distances between spatial firing rate maps, control within versus across condition; see Extended Data Fig. 2a for test by decoding, median and CIs (bootstrap)). g, Spatial versus task phase information content of all neurons and position and state encoding for example cells. Gray, sum-normalized histograms (color scale as in d).

Fig. 2. Recurrent neural dynamics can be used to navigate through locally ambiguous landmarks by forming and employing multimodal hypotheses.

a, Schematic examples of hypothesis-dependent landmark interpretation. Left, mouse encounters first LM, then identifies the second as ‘a’ based on the short relative distance. Right, a different path during LM1 leads the mouse to a different hypothesis state, and to identify the perceptually identical second landmark as ‘b.’ Hypothesis states preceding LM2 are denoted LM1_a and LM1_b, depending on the identity of the second landmark. b, Structure of an ANN trained on the task. Inputs encode velocity and landmarks. Right, mean absolute localization error averaged across test trials for random trajectories. c, Activity of output neurons ordered by preferred location shows transition between LM0, LM1 and LM2 phases. Red, true location. During LM1 (when the agent has only seen one landmark), two hypotheses are maintained, with convergence to a stable unimodal location estimate in LM2 after encountering the second landmark. d, 3D projection from PCA of ANN hidden neuron activities. During LM2, angular position in neural state space reflects position estimate encoding. e, Example ANN trajectories for two trials show how identical visual input (black arrowheads) leads the activity to travel to different locations on the LM2 attractor because of different preceding LM1_a/b states.

Fig. 3. Stable low-dimensional dynamics for hypothesis-based stimulus disambiguation.

a, Correlation structure in ANN activity is maintained across task phases, indicating maintained low-dimensional neural dynamics across different computational regimes. Top, pairwise ANN tuning correlations in LM1 and LM2 (same ordering, by preferred location). Bottom, tuning curve pairs (normalized amplitude). b, Same analysis as a, but for RSC in one session (N = 64 neurons, computed on entire spike trains, sorted via clustering in LM1). The reorganization of spatial coding as hypotheses are updated (Fig. 1d,f) is constrained by the stable pairwise structure of RSC activity. Neurons remain correlated (first and second pair) or anticorrelated (third and fourth pair) across LM1 and LM2. c, Summary statistics (session median and quartiles) for maintenance of correlations across task phases. This also extends to a separate visually guided dot-hunting task (Extended Data Fig. 8). d, Activity in both the ANN and RSC is locally low-dimensional, through correlation dimension (the number of points in a ball of some radius grows with radius to the power of N if data is locally N-dimensional) on 20 principal components. See Extended Data Fig. 8 for analysis by PCA.

Fig. 4. RSC exhibits stable attractor dynamics sufficient for computing hypothesis-dependent landmark identity.

a, Top, to study hypothesis encoding and its impact without sensory or motor confounds, we used trials with matched egocentric paths just before and after the second landmark (‘a’ or ‘b’) encounter. One example session is shown. Bottom, 3D neural state space trajectories (isomap); RSC latent states do not correspond directly to those of the ANN. b, RSC encodes the difference between LM1_a and LM1_b, and between subsequent LM2 states, as in the ANN (Fig. 2e and Extended Data Fig. 5). Blue, within-group and grey, across-group distances in neural state space. Horizontal lines, mean; boxes, 95% CIs (bootstrap). State can also be decoded from raw spike rates (Extended Data Fig. 9j). c, Neural dynamics in RSC are smooth across trials: pairwise distances between per trial spike counts in a 750 ms window before LM2 onset remain correlated with later windows; line, median; shading, CIs (bootstrap). d, RSC activity preceding the second landmark encounter predicts correct/incorrect port choice (horizontal line, mean; gray shaded box, 95% CI from bootstrap, cross-validated regression trees). e, Decoding of hypothesis states and position from RSC using ANNs to illustrate the evolution of neural activity in the task-relevant space (see b, c and d and Fig. 1e,f, Extended Data Fig. 9 statistics). f, Schematic of potential computational mechanisms. Left, if RSC encodes only current spatial and sensorimotor states and no hypotheses beyond landmark count (LM1_a or LM2_b, derived from seeing the first landmark and self-motion integration that lead to identifying the second landmark as ‘a’ or ‘b’), an external disambiguating input is needed. Right, because task-specific hypotheses arising from the learned relative position of the landmarks are encoded (this figure), and activity follows stable attractor dynamics (Fig. 3), ambiguous visual inputs can drive the neural activity to different positions, disambiguating landmark identity in RSC analogously to the ANN.

Extended Data Fig. 1. Task structure and behavioral data, and necessity of RSC for egocentric-allocentric computations.

(a) Schematic of task structure and timing. (b) Example trial schematic showing all possible task states (see Methods for more details). Landmarks were formed by white dots displayed on a screen which served as the floor of the arena. They were only made visible when mice crossed a distance threshold. Only one landmark was visible at a time in the final training stage. Nose-pokes were only registered after mice held their nose in the port for a randomly chosen delay period that was randomized for each visit and not known to the mouse. Incorrect port visits resulted in timeouts that were associated with a bright background across the entire arena. After each complete trial, which results in the reward state, mice are required to complete a separate task in which they need to ‘hunt’ for a series of 4 to 8 randomly placed blinking dots on the arena floor. Each dot disappears as soon as the mouse reaches it, resulting either in a new random annulus, or initialization of the next trial. The next trial begins with a new random rotation of the landmarks and rewarded port. (c) Training phases (see Methods). Mice are trained with a single landmark first, then 2 landmarks at unlimited view distance, and finally a limited view distance. (d) Top: Experimental setup for electrophysiology and real-time mouse position tracking. The arena was placed on top of a commercial flat-screen TV that was used to display visual landmarks. A motorized commutator was used to reduce tether-induced torque on the mouse, and a real-time optical tracking system was used to regulate the visibility of the landmarks and to identify when the mouse reached any of the blinking dots in the dot-hunting task. Bottom: view of the arena from the top, showing a subset of the reward ports as well as the tracking camera and the motorized commutator. (e) Example excerpt of behavioral data, with state transitions. Landmark visits (black arrowheads) are defined as the point when new landmarks become visible. (f) Top: Training curves for all 4 mice. The three major training phases are indicated with shading (corresponding to panel c). Red: Proportion of time that a landmark is visible (remains 1.0 (100%) until view distance is introduced). Blue: Maximum reward port hold time for each session, the actual hold times are drawn from a uniform distribution. Black: proportion of hits / false positives (corresponds to rewards / timeouts, or proportion correct), for the 1^st port visit in each trial. Values over 1/16 indicate that mice can distinguish the correct port amongst all ports. Values over 1 indicate that mice could reliably visit the correct port among the two ports indicated by locally ambiguous landmarks without excluding any other ports by trial and error (see main text and methods). Trials with 1^st landmark visit after <20 sec are included in analysis. Grey: Proportion of trials in which mice see both landmarks, and then turn around to go back to the 1^st landmark. If this proportion was 0, it would indicate that mice always visit the 2^nd port after seeing it, which would on average lead to chance-level behavioral performance. For each individual session, significance of correct choice for the 1^st port visit among the two indicated ports was tested with a binomial fit at the 95% level (two-sided, Clopper-Pearson exact method) and is indicated with a star. If the mouse also visited a large proportion of unmarked ports, this fraction can be significant despite the overall correct rate among all 16 ports being small. Bottom: latency to reward after encountering the 2^nd landmark in seconds (blue), proportion of visits to ‘a’ and ‘b’ as fraction of all port visits (orange) and proportion correct choice between ‘a’ or ‘b’ with binomial 95% CI (binomial as described before, green). See y-axis labels for unit definitions. (g) All paths taken by the mouse in one example session, split by LM0,1,2 state (green, glue, grey). (h) 6 example trials from the same session plotted from the start of the trial to the reward delivery, same color scheme as in g. 2 of the trials include time-outs (red). (i) Retrosplenial cortex is required for integrating egocentric sensory information and hypotheses about the animal’s allocentric location, but not for visually guided navigation. To causally test the role of RSC in relating spatial hypotheses to sensory data, we used a parametric allocentric/egocentric task using the same apparatus as in the main experiment and pharmacologically inactivated RSC. Schematic of task structure: Water restricted mice had to visit the port closest to a single visual landmark for a water reward. Visits to any other port resulted in a time-out, but allowed the mice to self-correct. As in the main experiment, the landmark and rewarded port were rotated randomly after each trial, forcing mice to use only the visual landmark. (j) To make the task reliant on allocentric hypotheses, we randomly varied the eccentricity of the landmark (center of the landmark to center of the arena, as fraction of the arena radius) at the beginning of each trial. Trials with low eccentricity (left) required the mouse to find the arena center (though path integration, requiring maintenance of a self-position hypothesis or memory in absence of persistence visual cues indicating the center of the arena) and then extrapolate a straight path through the landmark to the correct rewarded port. Alternatively, mice might triangulate which port is the closest to the landmark from the periphery. These strategies all require integration of self-location hypotheses with visual landmark information. Trials with high eccentricity (right) required merely walking to the port closest to the landmark. This design allowed us to test the role of RSC in the integration of location hypotheses with egocentric visual landmark information while simultaneously determining whether simpler visually-guided navigation was also affected. (k) RSC was either 1) transiently inactivated with Muscimol, 2) sham injected with cortex buffer, or 3) not injected (see methods). Each mouse was tested in both groups, with balanced ordering. (l) Task performance (mean and 95% confidence intervals for hit rate on 1^st port visits per trial, via binomial bootstrap). Mice always performed above full chance level (1/16^th, assuming they cannot make use of the landmark). Performance was selectively reduced by RSC inactivation for low eccentricity conditions where integration of location hypotheses and visual landmarks was required. Performance in the visually guided condition was only minimally affected.

Extended Data Fig. 2. The spatial code in RSC changes with hypothesis states, ANN and RSC neurons employ conjunctive codes, and preferentially represent landmark / reward locations.

(a) Location decoders (neural network, cross-validated per trial) do not generalize across landmark states, and LM1 carries less spatial information than LM2. Performance is measured by prediction likelihood in a 10×10 grid, means and shaded 95% CIs across sessions (N = 16 sessions). See Fig. 1f for test via spatial RF differences. (b) Left: Example ANN neuron tuning curves (from LM2) split by travel direction, speed, or location uncertainty (corresponding to LM0,1,2 states, derived from particle filter), showing conjunctive coding. Right: Three RSC example cells showing conjunctive coding of location vs. speed, and direction (Fig. 1d shows task phase vs. location). (c) Left: ANN neurons and, Right: RSC cells (N = 984 neurons) weakly preferentially fire at landmark locations. Top: distribution of locations where RSC cells fire most. Bottom: total average rates, split by LM1 and LM2. (d) Distribution of firing rates by angular position in the arena, same data as panel c. Blue: quantile of firing rates across population. Red: 95% CI of the mean across the population via bootstrap. Despite a small preference for the landmark locations, this effect is small compared to the overall variability on firing rates, and there is no systematic preference for cells to fire in proximity of one vs. the other landmark, even in the LM2 condition. (e) Information gain, which we study by analyzing landmark encounters, as transitions between LM_0,1,2 states throughout the manuscript, can also occur when mice fail to encounter a landmark where one would be expected given some hypothesis (see Fig. 2e for an ANN example). These cases can also be decoded from neural activity, but cannot be directly compared to landmark encounters, as they don’t offer the matched sensory input (that is no visual input vs. appearance of salient landmark) that we employ in Fig. 4 (mouse encounters 2^nd landmark, but it is either ‘a’ or ‘b’). These ‘virtual’ landmark encounters were decoded with a cross-validated NN on a trial level and compared to real landmark encounters. The same decoder was then cross tested on the reverse condition (grey plot) to show that the neural code for encounters and non-encounters is different, as is expected from the different sensory inputs. Analysis as in Extended Data Fig. 9a, but plots are aligned to the value at the 0-second point, see Methods for details.

Extended Data Fig. 3. Extracellular recording in mouse retrosplenial cortex.

(a) Tetrode drive implants targeting mouse retrosplenial cortex (RSC). See Methods for details. (b) Example band-passed (100Hz-5kHz) raw voltage traces from 16 tetrodes. (c) Verification of drive implant locations in RSC via histology in all 4 mice. White arrowheads indicate electrolytic lesion sites. (d) Histograms of mean firing rates of all 984 neurons across LM0 (green), LM1 (blue), and LM2 (black) conditions. Neurons are treated as independent samples. Overall rates did not shift significantly across these states. (e) Relative per-neuron changes in firing rates across conditions. Despite the lack of a population-wide shift in average rates, the firing rates of individual cells varied significantly across conditions with heterogeneous patterns of rates. Each grouping shows rates per cell, relative to the rate in LM0 (left) LM1 (middle), and LM2 (right) as individual rates (grey lines and histograms). Bar graphs show the 50% and 95% quantiles. (f) Spatial firing profiles of 42 example neurons split by hypothesis state. Number insets denote Max. firing rate in Hz per condition. For clarity, missing data is that was not due to exclusion via landmark visibility in LM1 is plotted as the darkest color in each plot. (g) Spatial firing rate profiles for all neurons from one example session (52 total), from the main task phase. Profiles were computed in 25×25 bins, and individually normalized to their 99^th percentile. (h) same as panel g, but from the separate trial initialization task (‘dot-hunting’) in which mice had to hunt for a series of blinking dots that appeared in random positions. (i) 36 example neurons from multiple sessions and animals, chosen to represent the broad range of tuning profiles. For each neuron, the main task tuning and the ‘dot-hunting’ are plotted together on the same brightness scale, normalized to their total maximal rate. In the dot-hunting task there is no conserved radial tuning due to the absence of consistent landmarks, however some cells retain angular spatial tuning due to olfactory cues in the arena. Tuning to eccentricity (distance to arena wall or center) is maintained across task phases in many neurons. Small numbers indicate maximum firing rates in Hz for each plot (color scale is same across the pairs).

Extended Data Fig. 4. Hypothesis encoding in RSC is task-specific and is a function of task learning.

(a) Foraging and dot-hunting tasks are interleaved, allowing comparisons of how the same neural population represents hypotheses. (b) We predict the number of encountered landmarks either within condition (for example foraging from foraging, each time using one trial as test, fitting to all others), or across. Only the first 2 landmarks were predicted to allow use of the same classifier across both despite the higher number of landmarks in the dot-hunting task. Train and test sets were split by trial. Decoding was done with a regression tree on low-pass filtered firing rates. Performance was quantified as mean error on the N of landmarks. (c) Example dot-hunting trial, the performance from using the foraging predictor is lower. (d) Summary stats from all sessions, means and bootstrapped CIs. The prediction is significantly better when using training data from the same category than when using the neural code from the other; for example dot-hunting to predict the foraging (P= ~0 / ~ 0 within vs. across categories for predicting dot-hunting and foraging landmark state), showing that hypothesis coding is task-specific. (e) To test whether hypothesis encoding is a specific function of task learning or a general feature of RSC, we examined whether coding persisted in case when mice performed the task but were not yet performing well. We first examined the ability to predict correct vs. incorrect port choice (same as in Fig. 4) as a function of per-session task performance. We analyzed data from sessions from the entire training period where the 2 landmarks were used, with at least 5 correct and 5 incorrect choices (N = 42 sessions), due to the closely spaced recordings, neurons might be re-recorded across sessions. On average we analyzed ~15-30 port visits per session (number of trials was unaffected by behavioral performance: CI of slope = [-7.7, 2.7], p = 0.33). Predictions were made as before with a test/train split on balanced hit/miss data with a regression tree. Prediction performance was at chance level ( ~ 47%, P = 0.81 vs. chance) for low performance sessions (total correct choice ratio of 0.8 or lower), and the same as in our initial analysis (Fig. 4) for sessions with high mouse performance ( ~ 66%, P = 0.00096 vs. chance). Overall, prediction performance was significantly correlated with task performance (P = 0.0014 vs. constant model). Individual mice are indicated with colored markers. (f) We also analyzed the more general decoding of landmark encounter count (same as Fig. 1) in all of the 92 sessions with 2 landmarks, and also found a significant correlation (p = 0.0045 vs. constant model), showing that hypothesis encoding throughout the task is driven by task learning. (g) As a control experiment, we tested whether decoding the number of landmarks encountered in the interleaved dot-hunting task might also be affected by task performance, if for instance the neural encoding and performance was a function of general spatial learning, habituation to the arena, motivation, etc., and we found this correlation to be flat (P = .6, CI for slope = [-0.17, 0.29]). We conclude that the encoding of hypothesis state is task-specific and a function of the mouse performing the task.

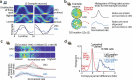
Extended Data Fig. 5. Architecture, trajectories, and population statistics for ANN with external map input.

(a) Structure of the recurrent network. Input neurons encoded noisy velocity input with linear tuning curves (similar to speed cells in the entorhinal cortex), and landmark information. In the standard setup (referred to as “external map”), the landmark input signaled the global configuration of landmarks (map). If there are K landmarks (all assumed to be perceptually indistinguishable), then whenever the animal encounters a landmark, the input provides a simultaneous encoding of all K landmark locations using spatially tuned input cells. Thus, the input encodes the map of the environment but does not disambiguate locations within it. This input can be thought of as originating from a distinct brain area that identifies the current environment and provides the network with its map. (b) Trajectories varied randomly and continuously in speed and direction. There were 2-4 landmarks at random locations. (c) Activity of output neurons ordered by preferred location as a function of time in an easy trial with two nearby landmarks and a constant velocity trajectory. Black arrows: landmark encounters. Thick black dashed line: time of disambiguation of location estimate in output layer. Thin red dashed line: true location. The network’s decision on when to collapse its estimate is flexible, and dynamically adapts the decision time to task difficulty: When the task is harder because of the configuration of landmarks (the task becomes harder as the two landmarks approach a 180 degree separation because of velocity noise and the resulting imprecision in estimating distances; the task is impossible at 180 degree because of symmetry), the network keeps alive multiple hypotheses about its states across more landmark encounters until it is able to reach an accurate decision. Panels c,d,f,g show example trials from experiment configuration 4 (See Methods) with different values of landmark separation parametrized by α. (d) Same as c, but in a difficult trial with two landmarks almost opposite of each other. (e) Top: The ANN took longer to disambiguate its location in harder task configurations: average time until disambiguation as a function of landmark separation (Standard error bars are narrower than line width). Middle: Distribution of the number of landmark encounters until the network disambiguates location, as a function of landmark separation. Bottom: Fraction of trials in which the network location estimate is closer to the correct than the alternative landmark location at the last landmark encounter, as a function of landmark separation. Data from 10000 trials in experiment configuration 4, 1000 for each of the 10 equally spaced values of α. The performance of the ANN (Fig. 2 main text) can be compared to the much poorer performance achieved by a strategy of path integration to update a single location estimate with landmark-based resets (to the coordinates of the landmark that is nearest the current path-integrated estimate), Fig. 2b (black versus gray). The latter strategy is equivalent to existing continuous attractor integration models^, combined with a landmark- or border based resetting mechanism^,,,, which to our knowledge is as far as models of brain localization circuits have gone in combining internal velocity-based estimates with external spatial cues. The present network goes beyond a simple resetting strategy, matching the performance of a sequential probabilistic estimator – the particle filter (PF) – which updates samples from a multi-peaked probability distribution over possible locations over time and is asymptotically Bayes-optimal (M = 1000 particles versus N = 128 neurons in network; Fig. 2b, lavender (PF) and green (enhanced PF)). Notably, the network matches PF performance without using stochastic or sampling-based representations, which have been proposed as possible neural mechanisms for probabilistic computation^,. (f) Similar to c, but in a trial where the network disambiguates its location before the second landmark encounter. Yellow arrows mark times of landmark interactions if the alternative location hypothesis had been correct. Disambiguation occurs shortly after the absence of a landmark encounter at the first yellow arrow. (g) Similar to f, but in a trial where disambiguation occurs at the first landmark location, since no landmark has been encountered at the time denoted by the first gray arrow. (h) In the regular task where landmark identity must be inferred by the ANN, discrete hypothesis states (denoted LM0,1,2 throughout) emerge during the LM1 state. (j) If the ANN is instead given the landmark identity via separate input channels, it immediately identifies the correct location after the 1^st landmark encounter and learns to acts as a simple path integration attractor without hypothesis states. Plots show ANN output as in c,d,g,f. (i,k) To quantify the separation of hypothesis states in the ANNs hidden states even in cases where such separation might not be evident in a PCA projection, we linearly projected hidden state activations onto the axis that separates the hypothesis states. The regular ANN shows a clear LM1 vs LM2 separation, but the ANN trained with landmark identity does not distinguish between these. (l) Population statistics for ANN with external map input. Scatter plot of enhanced particle filter (ePF) circular variance vs. estimate decoded from hidden layer of the network. 4000 trials from experiment configuration 1 were used to train a linear decoder on the posterior circular variance of the ePF from the activity of the hidden units and performance was evaluated on 1000 test trials. (m) Scatter plot of widths and heights of ANN tuning curves after the 2^nd landmark encounter. Insets: example tuning curves corresponding to red dots. Unlike hand-designed continuous attractor networks, where neurons typically display homogeneous tuning across cells^,,, our model reproduces the heterogeneity observed in hippocampus and associated cortical areas. Tuning curves are from LM2 using 1000 trials from experiment configuration 2 using 20 location bins. Tuning height specifies the difference between the tuning curve maximum and minimum, and tuning width denotes the fraction of the tuning curve above the mean of maximum and minimum. (n) The distribution of recurrent weights shows that groups of neurons with strong or weak location tuning or selectivity have similar patterns and strengths of connectivity within and between groups: distribution of absolute connection strength between and across location-sensitive “place cells” (PCs) and location-insensitive “unselective cells” (UCs) in the ANN. The black line denotes the mean; s.e.m. is smaller than the linewidth. The result is consistent with data suggesting that place cells and non-place cells do not form distinct sub-networks, but are part of a system that collectively encodes more than just place information. Location tuning curves were determined after the second landmark encounter using 5000 trials from distribution 1 and using 20 location bins. The resulting tuning curves were shifted to have minimum value 0 and normalized to sum to one. The location entropy of each neuron was defined to be the entropy of the normalized location tuning curve. Neurons were split in two equal sets according to their location entropy, where neurons with low entropy were defined as “place cells” (PCs) and neurons with high entropy were defined as “non-place cells” (UCs). Between and across PCs and UCs absolute connection strength was calculated as the absolute value of the recurrent weight between non-identical pairs. (o) Pairwise correlation structure is maintained across LM[1,2] states and environments. Corresponds to Fig. 3a. Top: Correlations in spatial tuning between pairs of cells in one environment after the 1^st landmark encounter / LM1 (left), after the 2^nd encounter / LM2, and in a separate environment in LM2 (right). The neurons are ordered according to their preferred locations in environment 1. Bottom: Example tuning curve pairs (normalized amplitude) corresponding to the indicated locations i-iv. Data from experiment configuration 1. (p) State-space activity of ANN is approximately 3-dimensional. Even when summed across all environments and random trajectories, the states still occupy a very low-dimensional subspace of the full state space, quantified by the correlation dimension as d ≈ 3 (left, see Methods). This measure typically overestimates manifold dimension, and serves as an upper bound on the true manifold dimension. As a control, the method yields a much larger dimension (d = 14) on the same network architecture with large random recurrent weights (right); thus, the low-dimensional dynamics are an emergent property of the network when it is trained on the navigation task. Data from 5000 trial, recurrent weights were sampled i.i.d. from a uniform distribution W_h,ij ~ U([ − 1, 1]), then fixed across trials. The initial hidden state across trials was sampled from h_t=0,i ~ U([ − 1, 1]). Data from 5000 trials from experiment configuration 1. (q) In the LM2 state, position on the rate-space attractor corresponds to location in the maze. State-space trajectories after second landmark encounter for random trajectories. Color corresponds to true location (plot shows 100 trials). (r) ANN with external map input implements a circular attractor structure: Hidden layer activity arranged by preferred location in an example trial shows a bump of activity that moves coherently. Black arrows: first two landmark encounters. Preferred location was determined after the second landmark encounter using 5000 trials from experiment configuration 1. (s) Left: Recurrent weight matrix arranged by preferred location of neurons (determined after the second landmark encounter using 5000 trials from experiment configuration 1) indicates no apparent ring structure, despite apparent bump of activity that moves with velocity inputs (panel a). Right: However, recurrent coupling of modes defined by output weights (defined by $W_{\mathit{out}}{W}_{\mathit{rec}}{W}_{\mathit{out}}^T$, where $W_{\mathit{rec}}$ are the recurrent weights and $W_{\mathit{out}}$ are the output weights) has a clear band structure. Connections between appropriate neural mixtures in the hidden layer – defined by the output projection of the neurons – therefore exhibit a circulant structure, but the actual recurrent weights do not, even after sorting neurons according to their preferred locations. The ANN thus implements a generalization of hand-wired attractor networks, in which the integration of velocity inputs by the recurrent weights occurs in a basis shuffled by an arbitrary linear transformation. Given these results, one cannot expect a connectomic reconstruction of a recurrent circuit to display an ordered matrix structure even when the dynamics are low-dimensional, without considering the output projection. Because trials in the mouse experiments typically ended almost immediately when the mouse had seen both landmarks (See Extended Data Fig. 1f for a quantification), we did not quantify the topology of the neural dynamics in RSC. (t) Low-dimensional state-space dynamics in the ANN with external map input suggests novel form of probabilistic encoding. Visualization of the full state-space dynamics of the hidden layer population, projected onto the three largest principal components, for constant-velocity trajectories. ANN hidden layer activity was low-dimensional: Fig. 3a shows data on low-dimensional dynamics, evident in maintained pairwise correlations, and Fig. 3d and panel p show correlation dimension. Trajectories are shown from the beginning of the trials; arrows indicate landmark encounter locations, black squares: first landmark encounter; black circles: second landmark encounter; line colors denote trajectory stage: LM0 (green), LM1 (blue), andLM2 (grey). Data in a-c is from 1000 trials from experiment configuration 3 (see Methods); sensory noise was set to zero. Trajectory starting points were selected to be a fixed distance before the first landmark. The intermediate ring (LM1) corresponds to times at which the output neurons represent multiple hypotheses, whereas the final location-coding ring (LM2), well-separated from the multiple hypothesis coding ring, corresponds to the period during which the output estimate has collapsed to a single hypothesis. In other words, the network internally encodes single-location hypothesis states separably from multi-location hypothesis states, as we find in RSC (Fig. 1), and transitions smoothly between them, a novel form of encoding of probability distributions that appears distinct from previously suggested forms of probabilistic representation^,. (u) ANN trial trajectory examples, (corresponding to Fig. 2e). Divergence of trajectories for two paths that are idiothetically identical until after the second landmark encounter. ‘a’ and ‘b’ denote identities of locally ambiguous identical landmarks. Disambiguation occurs at the second landmark encounter, or by encountering locations where a landmark would be expected in the opposite identity assignments. See insets for geometry of trajectories and landmark locations. LM2 state has been simplified in these plots. (v) All four trajectories from panel b plotted simultaneously, and with full corresponding LM2 state. (w) The low-dimensional state-space manifold is stable, attracting perturbed states back to it, which suggests that the network dynamics follow a low-dimensional continuous attractor and the network’s computations are robust to most types of noise. Relaxations in state space after perturbations before the first (left), between first and second (middle), and after the second (right) landmark encounter. For the base trial, a trial with two landmarks and random trajectory was chosen. The first and second landmark encounter in this base trial is at time t = 2 s and t = 4.6 s respectively. At time t = 1 s (left), t = 4 s (middle), and t = 7 s (right) a multiplicative perturbation of size 50% was introduced at the hidden layer. See Extended Data Fig. 10l for same result on internal map ANNs.

Extended Data Fig. 6. ANN and RSC coding transitions dynamically from an egocentric landmark-relative to an allocentric global reference frame based on phase in trial.

(a) Top: Tuning curves (mean rate) for displacement from last encountered landmark for LM1 and LM2 states in ANN. Bottom: Same data, but distribution of firing rates. The network discovers that displacement from the last landmark encounter in the LM1 period is a key latent variable, and its encoding is an emergent property. Intriguingly, a similar displacement-to-location coding switch has been observed in mouse CA1, suggesting that the empirically observed switch may be related to the brain performing spatial reasoning to disambiguate between multiple location hypotheses. (b) Same as panel a but for global location, ANN neurons became more tuned to global location rather than landmark-relative information after encountering the 2^nd landmark. (c) Decoding of location, displacement, and separation between landmarks from the ANN in a 2-landmark environment by a linear decoder that remains fixed across trials and environments. Top: Squared population decoding error of location (green) and displacement (blue), as a function of the number of encountered landmarks. As suggested by the well-tuned activity of ANN neurons, location can be linearly decoded in the LM2 state. Displacement can be best decoded in the LM1 state. Bottom: Square decoding error of distance between landmarks, as a function of the number of encountered landmarks. The representation is particularly accurate around the time just before and after the first landmark encounter, when location disambiguation takes place. Top: Performance was evaluated on 1000 trials from experiment configuration 2. For location, the decoder corresponded to the network location estimate. For displacement, the linear decoder was trained on 4000 separate trials. Bottom: experiment configuration 1 with 4000 trials to train the linear decoder and 1000 trials to evaluate it. Thus, the network’s encoding of these three critical variables is dynamic and tied to the different computational imperatives at each stage: displacement and landmark separation are not explicit inputs but the network estimates these and represents them in a decodable way at LM1, the critical time when this information is essential to the computation. After LM2, the network decodability of landmark separation drops, as it is no longer essential. (d) Neurons in RSC also became less well tuned to relative displacements from landmarks in LM2 relative to LM1: histogram across all RSC neurons of entropy of tuning curve for angular displacement from last seen landmark in RSC. Black: for LM2 state, Blue: for LM1 state. Red: histogram of pairwise differences. For this analysis, angular firing rate distributions were analyzed relative to either the global reference frame or the last seen landmark. (e) Same as d, but for global location. (f) The absolute change in landmark-relative displacement coding (d) is larger than that of the allocentric location tuning (e), suggesting that the latter is less affected by task state.

Extended Data Fig. 7. In addition to explicitly encoding number of visited landmarks, RSC and the ANN exhibit higher trial-to-trial variability in partial information states.

(a) Bottom: Mean spatial activity profile of 2 example ANN neurons for LM1 and LM2. Average tuning is higher for the LM2 state. Top: same data as histograms, showing that the less well-tuned LM1 state corresponds to a bimodal rate distribution (rates are high in some trials, low in others) that transitions to a unimodal distribution once the 2^nd landmark has been identified in LM2. Data are from experiment configuration 2 (See Methods, section ‘Overview over experiment configurations used with ANNs’). Tuning curves were calculated using 20 bins of location/displacements and normalized individually for each neuron. The first time step in each trial and time steps with non-zero landmark input were excluded from the analysis. For histograms, each condition was binned in 100 column bins and neuron rates in 10 row bins. Histograms were normalized to equal sum per column. (b) Similarly, RSC rates are more dispersed per location in LM1. Schematic of analysis: firing rates were low pass filtered at 0.5 Hz, and for each location, the distribution of rates was computed in 8 bins, between the lowest and highest rate of that cell. (c) Example analysis for one cell. Top: Rate distribution resolved by 2D-location (4×4 bins) for example RSC neuron. Bottom: the resulting 16 histograms for LM1 and LM2 each, red dotted example histograms correspond to indicated example location (red dotted circles). (d) Summary statistics showing a more dispersed rate distribution per location in LM1. In sum, this analysis shows that in addition to the explicit encoding of uncertainty by a stable rate code (conjunctive with position and other variables), as shown in Fig. 1d,e,f and Extended Data Fig. 2a, where one would not expect a higher degree of trial-to-trial variability with higher uncertainty, there is still a degree of increased variability in states where the mouse might ‘take a guess’ that would differ between trials. This parallels a similar behavior in the ANN (panel a).

Extended Data Fig. 8. Pairwise rate correlation structure in RSC is maintained across LM1 and LM2 states.

(a) Low-dimensional population structure can be probed by pairwise neural relationships: correlations or offsets in spatial tuning between cell pairs should be preserved across environments if the dynamics across environments is low-dimensional. Example spike rates (6 sec window, low-passed at 1 Hz using a single-pole Butterworth filter) for 3 RSC neuron pairs from one example session. R values for each pair were computed across the LM1 and LM2 condition, as well as in the task-initialization phase where mice had to hunt blinking dots (Extended Data Figs. 1, 4). The latter provides a control condition where no landmark-based navigation was required and mice instead had to walk to randomly appearing targets. (b) Top: pairwise correlation matrices for LM1,2 and dot-hunting conditions. Example pairs are highlighted (i,ii,iii). Bottom: spatial firing rate profiles for example pairs. Same analysis as in Fig. 3a. (c) RSC activity is globally low-dimensional. Proportion of variance of low-pass filtered (0.5 Hz) firing rates explained by first 45 principal components from the LM1 states. Proportion of variance explained (black, 16 sessions) drops to below that of shuffled spike trains (red) after the 6-10^th principal component. The inset shows the analysis split by condition (same as in panels a and b), and 95% Cis for the spectra across sessions. The right panel shows zoomed in region of the same plot. We found no relationship between individual PCA components and task variables. (d) Correlation dimension in RSC is also low (same analysis as for the ANN in Extended Data Fig. 5p). This measure typically overestimates manifold dimension, and thus serves as an upper bound on the true manifold dimension. (e) Grey/black: Summary statistics (median and quartiles) for correlation of correlations (panel b shows one example session, black dots indicate individual sessions, N = 16). Median of R value of R values for LM1 vs. LM2 = 0.74 (corresponding R in ANN = 0.73), for LM1 vs. dot-hunting = 0.51. Green: same analysis but spike rates were computed with a 5 Hz low-pass instead of the 1 Hz used throughout, no systematic changes were observed as function of low-pass settings. (f) Rates of individual RSC neurons can be predicted from other neurons with linear regression. In the LM2 to LM2 condition (black), the linear fit is computed for one held-out neuron’s rate from other concurrent rates, and the same regression weights are then used to predict rates during LM1 (green) and dot-hunting (red) time periods. True rates of predicted neurons are plotted as solid black lines. (g) Summary statistics for the linear regression. Histograms show the proportion of explained variance for all 984 neurons, split by condition. In the LM2 to LM2 condition, the fit is computed from other concurrent rates (40.5% variance explained, median across neurons). In the two other conditions, the regression weights are fit in LM2 and held fixed. The sequential, non-interleaved nature of this train/test split across task phases means that any consistent firing rate drifts across the conditions will lead to poor predictions, and consequently, a small number of neurons exhibit negative R² values indicating a fit that can, for some cells, be worse than an average rate model (11.3% for LM1, 19.3% median across neurons for dot-hunting, small grey bars). However, 24.3% of variance (median across neurons) can be explained despite significant changes in spatial receptive fields (predict LM1 with LM2 weights) and even for a different task, with 16.2% when predicting dot-hunting activity from LM2 weights (red and green histogram and bars showing 95% CI of median). (h) Pairwise correlations between RSC neurons in another example session, same analysis as in panel b, and associated scatterplots. (i) Low-dimensional activity quantified via participation ratio (PR). This analysis does not account for noisy eigenvalue estimates from spiketrains, and consequently the shuffled spike trains where there are no prominent modes that correspond to stable sensory, motor, or latent states, yield values of PR = ~ 45.

Extended Data Fig. 9. Low-dimensional spatial modes of mouse RSC activity.

(a) Top left: the speed at which the neural activity evolves (avg. speed of largest 5 principal components, filtered at 1 Hz, CIs via bootstrap) correlates with running speed. Top right: When landmarks appear/disappear, they perturb neural activity (effect of mouse speed is regressed out). Bottom: Analysis of the time course of the prediction of LM0,1,2 state from RSC firing rates around the time when the landmarks appeared. Plots show 95% CIs for the mean of the state prediction, aligned to the mean, corresponding to a de-biased state estimation probability over time. Decoding was performed using the same method as in Fig. 1. (b) For some analyses of the low-dimensional dynamics in RSC (Fig. 4, this figure panel h), rate fluctuations related to non-spatial covariates such as speed, heading, etc. were removed: a single-layer LSTM with 20 hidden units was trained to predict the mouse position in a 10×10 grid from the RSC rates. The network learned 20 spatially relevant mixtures of input firing rates, with appropriate temporal smoothing to represent the mouse location. These activations were then embedded into 3-D space via isomap. (c) To find trials across which mouse trajectories as they approached the 2^nd landmark were similar, mouse trajectories were clustered (see Methods) leading to a subset of trials with similar locomotion and visual inputs. (d) The activity of RSC, in the low-dimensional representation, and in raw spike counts was then analyzed further. The example plot shows low-dimensional neural trajectories from LM0,1,2 states during matched mouse trajectories. (e) Alternative hypotheses for smoothness / predictability of neural dynamics across trials (corresponding to Fig. 4c). Dynamics across trials could behave like a laminar flow, so that trials with similar neural state remain so (top), or they could shuffle, leading to a loss of the pairwise distance relationships across trials (bottom). (f) We measured this maintenance vs. loss of correlation in a sliding 750 ms window beginning at the 2^nd landmark onset, versus a window just before. CIs were computed across sessions (See Methods). (g) Hypotheses for whether stable neural dynamics (Fig. 3b,c, Extended Data Fig. 8) can determine how RSC activity encodes disambiguated landmark identity (‘a’ or ‘b’). Top: trials in which the correct identity is ‘a’ but that are neurally close to other trials where the answer is ‘b’ might get dragged along in the wrong direction at least transiently. This would indicate relevance of recurrent dynamics on this computation. Bottom: alternatively, neural activity could be determined by the correct answer, even in trials that (in neural rate space) are close to trials from the opposing class. (h) We tested this by finding the closest trial from the opposing class (for example the closest LM1_a for a LM1_b trial) in the 3-D embedded (via Isomap) RSC rate space. To evaluate co-evolution regardless of this selection confound, we then analyzed the direction of flow of the neural state over time (red). As a control, we also analyzed neurally far trials (grey). The flow direction of the neural activity was significantly aligned for ~100 ms. Median and CI via bootstrap. (i) Left: Schematic for the analysis of representation of LM1_a vs. LM1_b states. Trial-to-trial distances were compared within group vs. across group. Right: Both before and after the 2^nd landmark becomes visible, the classes are distinct in neural state space. (Same data as in Fig. 4b, 5 sessions, 101 matched trials). (j) Whether a trial comes from LM1_a or _b can also be decoded from low-pass filtered (2 Hz) firing rates before the 2^nd landmark onset (via regression tree, cross-validated across trials, balanced N across conditions, 5 sessions).

Extended Data Fig. 10. ANN with binary landmark presence input, and ANN with non-negative rates, recapitulates all main findings from the external map ANN.

(a) ANN with binary landmark presence input. Here, the ANN must simultaneously infer the landmark locations and the location of the animal, in contrast to the previous “external map” configuration. These determinations are inter-related, thus the much higher difficulty of the task. Structure of the recurrent network. Input neurons encoded noisy velocity (10 neurons) and landmark information (1 neuron). In the internal map setup, the input signaled whether a landmark was present at the current position or not. (b) State space trajectories in the internal map network after the second landmark encounter in two different environments. The dark green / dark blue parts of the trajectories correspond to the sections before the third landmark encounter. Left: Predominantly counterclockwise trajectories, right: Predominantly clockwise trajectories. Landmarks and trajectories were sampled with the same parameters as experiment configuration 1, but the duration of test trials was extended from 10 s (100 timesteps) to 50 s (500 timesteps). Only trials with low error after the second landmark encounter are shown, defined as maximum network localization error smaller than 0.5 rad, measured in a time window between 5 timesteps after the second landmark encounter until the end of the trial. Only the state-space trajectory after the second landmark encounter is displayed. (c) State space dimension is approximately 3, same analysis as in Extended Data Fig. 5p. (d) Example tuning curves, same analysis as in Extended Data Fig. 5m. (e) Linear decoding of position, displacement from last landmark and landmark separation from ANN activity, same analysis as in Extended Data Fig. 6c. A multinomial regression decoder was trained on 4000 trials from experiment configuration 1 (the training distribution of the internal map task) to predict from hidden layer activities which of the four possible environments was present. Performance was evaluated on separate 1000 test trials sampled from the training distribution. (f) Example neurons showing transition from egocentric landmark-relative displacement coding to allocentric location encoding, same analysis as in Extended Data Fig. 6a,b. (g) Example neurons showing conjunctive encoding, same analysis as in Extended Data Fig. 2b. Location tuning curves were determined after the second landmark encounter using 1000 trials from experiment configuration 2 using 20 location bins. Velocity and uncertainty from the posterior circular variance of the enhanced particle filter were binned in three equal bins. (h) Distribution of absolute connection strength between and across location-sensitive “place cells” (PCs) and location-insensitive “unselective cells” (UCs), same analysis as in Extended Data Fig. 5n. (i) Hidden unit activations, corresponding to Fig. 2d. (j) Trajectories from example trials, as in Fig. 2e. (k) Same trajectories as in i&j but with full LM2 state. (l) ANN is robust to perturbations, same as in Extended Data Fig. 5w. (m) ANN maintains pairwise correlation structure across states and environments, same as in Fig. 3a and Extended Data Fig. 5o. (n) ANN with non-negative rates recapitulates the main findings from the conventional ANNs. Training an ANN in the external map condition but with non-negative activity replicated all key results from the other NN types: we observed similar results with respect to location and displacement tuning (r), the transition in linear decodability of displacement to location from the population and dynamically varying decodability of landmark separations within trials (p), the presence of heterogeneous and conjunctive tuning (s), lack of modularity in connectivity between cells with high and low amounts of spatial selectivity (t), and the preservation of cell-to-cell correlations across time within trials and across environments (q). The nonlinearity does affect the distribution of recurrent weights: The distribution of non-diagonal elements in the non-negative network is sparse (excess kurtosis k = 7.8), while it is close to Gaussian for the external and internal map networks with tanh-nonlinearity (k = 0.6 and k = 0.9 respectively; panel u); however, the distributions of eigenvalues of the recurrent weights have similar characteristics for all trained networks (panel v). Structure of the recurrent network: Input neurons encoded noisy velocity (10 neurons) and received external map input (70 neuron), same as the regular external map ANN. Recurrent layer rates were constrained to be non-negative. (o) Example tuning curves, same analysis as before. (p)Linear decoding of position, displacement from last landmark and landmark separation from ANN activity, same analysis as before. (q) ANN maintains pairwise correlation structure across states and environments, same as before. (r) Example neurons showing transition from egocentric landmark-relative displacement coding to allocentric location encoding, same analysis as before. (s) Example neurons showing conjunctive encoding, same analysis before. (t) Distribution of absolute connection strength between and across location-sensitive “place cells” (PCs) and location-insensitive “unselective cells” (UCs), same analysis as before. (u) Distribution of non-diagonal recurrent weights for randomly initialized (untrained), external map, internal map, and non-negative network. The k-value measured denotes excess kurtosis, a measure of deviation from Gaussianity (k = 0 for Gaussian distributions). The presence of a nonlinearity constraint on the ANN affects the distribution of recurrent weights: The distribution of non-diagonal elements in the non-negative network is sparse (excess kurtosis k = 7.8), while it is close to Gaussian for the external and internal map networks with tanh-nonlinearity (k = 0.6 and k = 0.9 respectively). (v) Scatterplot of real and imaginary part of complex eigenvalues of recurrent weight matrix for randomly initialized (untrained), external map, internal map, and non-negative network. The distributions of eigenvalues of the recurrent weights have similar characteristics for all trained networks.