Reconstructing rearrangement phylogenies of natural genomes
- PMID: 40483529
- PMCID: PMC12144824
- DOI: 10.1186/s13015-025-00279-5
Reconstructing rearrangement phylogenies of natural genomes
Abstract
Background: We study the classical problem of inferring ancestral genomes from a set of extant genomes under a given phylogeny, known as the Small Parsimony Problem (SPP). Genomes are represented as sequences of oriented markers, organized in one or more linear or circular chromosomes. Any marker may appear in several copies, without restriction on orientation or genomic location, known as the natural genomes model. Evolutionary events along the branches of the phylogeny encompass large scale rearrangements, including segmental inversions, translocations, gain and loss (DCJ-indel model). Even under simpler rearrangement models, such as the classical breakpoint model without duplicates, the SPP is computationally intractable. Nevertheless, the SPP for natural genomes under the DCJ-indel model has been studied recently, with limited success.
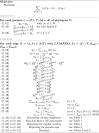
Methods: Building on prior work, we present a highly optimized ILP that is able to solve the SPP for sufficiently small phylogenies and gene families. A notable improvement w.r.t. the previous result is an optimized way of handling both circular and linear chromosomes. This is especially relevant to the SPP, since the chromosomal structure of ancestral genomes is unknown and the solution space for this chromosomal structure is typically large.
Results: We benchmark our method on simulated and real data. On simulated phylogenies we observe a considerable performance improvement on problems that include linear chromosomes. And even when the ground truth contains only one circular chromosome per genome, our method outperforms its predecessor due to its optimized handling of the solution space. The practical advantage becomes also visible in an analysis of seven Anopheles taxa.
Keywords: Ancestral reconstruction; Double-cut-and-join; Genome rearrangement; Integer linear programming; Small parsimony.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare no competing interests.
Figures

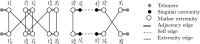









References
-
- Braga MDV, Willing E, Stoye J. Double cut and join with insertions and deletions. J Comput Biol. 2011;18(9):1167–84. 10.1089/cmb.2011.0118. - PubMed
-
- Yancopoulos S, Attie O, Friedberg R. Efficient sorting of genomic permutations by translocation, inversion and block interchange. Bioinformatics. 2005;21(16):3340–6. 10.1093/bioinformatics/bti535. - PubMed
-
- Doerr D, Chauve C. Small parsimony for natural genomes in the DCJ-indel model. J Bioinform Comput Biol. 2021;19(06):2140009. 10.1142/S0219720021400096. - PubMed
LinkOut - more resources
Full Text Sources
Miscellaneous

