Conductivity of Filled Diblock Copolymer Systems: Identifying the Main Influencing Factors
- PMID: 40508745
- PMCID: PMC12158064
- DOI: 10.3390/polym17111502
Conductivity of Filled Diblock Copolymer Systems: Identifying the Main Influencing Factors
Abstract
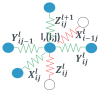
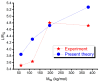
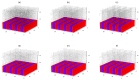
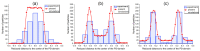
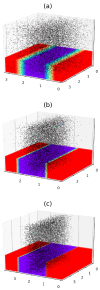
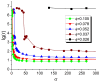
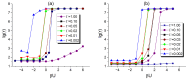
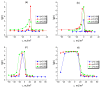
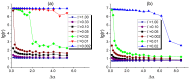
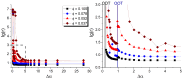
By developing and making use of the multi-scale theoretical approach, we identify the main factors that affect the conductivity of a composite composed of a diblock copolymer (DBC) system and conductive particles. This approach relies on the consistent phase-field model of DBC, Monte-Carlo simulations of the filler localization in DBC, and the resistor network model that mimics the conductive filler network formed in DBC. Based on the described approach, we thoroughly explore the relation among the morphological state of the microphase-separated DBC, localization of fillers in DBC, and the electrical response of the composite. Good agreement with experimental results confirms the accuracy of our theoretical predictions regarding the localization of fillers in the DBC microphases. The main factors affecting the composite conductivity are found to be: (i) affinities of fillers for copolymer blocks; (ii) degree of the segregation of a host DBC system, driven by external stimuli; (iii) geometry of the microphases formed in the microphase-separated DBC; and (iv) interactions between fillers. The conductor-insulator transition in the filler network is found to be caused by the order-disorder transition in the symmetric DBC. The order-order transition between the ordered lamellae and cylindrical microphases of asymmetric DBC causes a spike in the composite conductivity.
Keywords: conduction; diblock copolymers; fillers.
Conflict of interest statement
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Figures

Similar articles
-
Effect of the Interplay between Polymer-Filler and Filler-Filler Interactions on the Conductivity of a Filled Diblock Copolymer System.Polymers (Basel). 2023 Dec 29;16(1):104. doi: 10.3390/polym16010104. Polymers (Basel). 2023. PMID: 38201769 Free PMC article.
-
Conductivity of Insulating Diblock Copolymer System Filled with Conductive Particles Having Different Affinities for Dissimilar Copolymer Blocks.Polymers (Basel). 2020 Jul 25;12(8):1659. doi: 10.3390/polym12081659. Polymers (Basel). 2020. PMID: 32722506 Free PMC article.
-
Temperature dependence of the conductivity of filled diblock copolymers.Phys Rev E. 2020 Nov;102(5-1):052504. doi: 10.1103/PhysRevE.102.052504. Phys Rev E. 2020. PMID: 33327154
-
A Review of Polymer Composites Based on Carbon Fillers for Thermal Management Applications: Design, Preparation, and Properties.Polymers (Basel). 2021 Apr 16;13(8):1312. doi: 10.3390/polym13081312. Polymers (Basel). 2021. PMID: 33923627 Free PMC article. Review.
-
Structural, electrical, and physical-mechanical properties of composites obtained based on filled polyolefins and thermoplastic elastomers.RSC Adv. 2025 Feb 27;15(9):6541-6563. doi: 10.1039/d5ra00105f. eCollection 2025 Feb 26. RSC Adv. 2025. PMID: 40017642 Free PMC article. Review.
References
-
- Huh J., Ginzburg V., Balazs A. Thermodynamic behavior of particle/diblock copolymer mixtures: Simulation and theory. Macromolecules. 2000;33:8085–8096. doi: 10.1021/ma000708y. - DOI
-
- Chervanyov A.I., Balazs A. Effect of particle size and shape on the order-disorder phase transition in diblock copolymers. J. Chem. Phys. 2003;119:3529–3534. doi: 10.1063/1.1591723. - DOI
-
- Heinrich G., Kluppel M., Vilgis T. Reinforcement of elastomers. Curr. Opin. Solid State Mater. Sci. 2002;6:195–203. doi: 10.1016/S1359-0286(02)00030-X. - DOI
-
- Alig I., Skipa T., Engel M., Lellinger D., Pegel S., Poetschke P. Electrical conductivity recovery in carbon nanotube polymer composites after transient shear. Phys. Status Solidi B-Basic Solid State Phys. 2007;244:4223–4226. doi: 10.1002/pssb.200776138. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

