Synthetic Lagrangian turbulence by generative diffusion models

Abstract

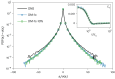
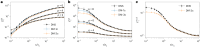
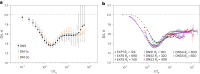
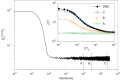
Lagrangian turbulence lies at the core of numerous applied and fundamental problems related to the physics of dispersion and mixing in engineering, biofluids, the atmosphere, oceans and astrophysics. Despite exceptional theoretical, numerical and experimental efforts conducted over the past 30 years, no existing models are capable of faithfully reproducing statistical and topological properties exhibited by particle trajectories in turbulence. We propose a machine learning approach, based on a state-of-the-art diffusion model, to generate single-particle trajectories in three-dimensional turbulence at high Reynolds numbers, thereby bypassing the need for direct numerical simulations or experiments to obtain reliable Lagrangian data. Our model demonstrates the ability to reproduce most statistical benchmarks across time scales, including the fat-tail distribution for velocity increments, the anomalous power law and the increased intermittency around the dissipative scale. Slight deviations are observed below the dissipative scale, particularly in the acceleration and flatness statistics. Surprisingly, the model exhibits strong generalizability for extreme events, producing events of higher intensity and rarity that still match the realistic statistics. This paves the way for producing synthetic high-quality datasets for pretraining various downstream applications of Lagrangian turbulence.

Keywords: Fluid dynamics; Statistical physics.

Fig. 1. Comparison between DNSs and DMs.

a, Standardized PDFs of one generic component of the velocity increment, δ_τV_i, at τ/τ_η = 1, 2, 5, 100 for ground-truth DNS data (black lines), synthetically generated data from DM-1c (blue lines with circles) and that from DM-1c-10% (green lines with squares), a DM-1c model trained with 10% DNS data. PDFs for different τ are vertically shifted for the sake of presentation. σ is the standard deviation. b–d, DM-1c trajectories for one generic velocity component with large (b), medium (c) and small (d) time increments, τ/τ_η = 100, 5, 1, respectively. e, Comparison of 3D trajectories showing small-scale vortex structures for both DNS and DM-3c data, where different curves correspond to the three standardized velocity components i = x, y, z. For the DNS, the high oscillatory correlations between the three components are consistent with the presence of strong vortical structures. Similarly, in the case of DM-3c, these correlations can be interpreted as reflecting vortical structures within the hypothetical Eulerian flow. f, Examples of 3D trajectories reconstructed from DNS (bottom) and DM-3c (top). Notice in panel a the remarkable generalizability properties of our DM data-driven model, able to explore and capture extreme events for velocity fluctuations with far larger intensities than observed in the DNS dataset, represented by much more extended tails, while still maintaining the ground-truth statistics inherent in the training data. Here, the statistics for DM-1c and DM-1c-10% data are derived from 86 and 22 times the number of trajectories in the DNS, respectively. Source data

Fig. 2. Statistics of acceleration.

Standardized PDFs of one generic component of the acceleration, a_i, for ground-truth DNS data (black line), synthetically generated data from DM-1c (blue line with circles) and that from DM-1c-10% (green line with squares). Notice the ability of DM-1c to well generalize the statistical trend for rare intense fluctuations never experienced during the training phase with the DNS data. The statistics of the DM-1c and DM-1c-10% data are based on 86 and 22 times the number of trajectories in the DNS, respectively. Inset: acceleration correlation function. Source data

Fig. 3. Illustration of the DM and in-depth examination of its backward generation process.

a, Schematic representation of the DM and associated UNet sketch, complemented by a table of hyperparameters. Here, N denotes the total number of diffusion steps and n denotes the intermediate step. More details on the network architecture can be found in the Methods section and ref. . b, Three distinct noise schedules for the DM’s forward and backward processes explored in this study (Methods). Points A–D indicate four different stages during the backward generation process (from ${\mathcal{V}}_N$ to ${\mathcal{V}}_0$) along the optimal noise schedule, curve (tanh6-1). At an early step during the backward process, we have very noisy signals, n = 0.52N (D), followed by two intermediate steps at n = 0.27N (C) and n = 0.06N (B) and the final synthetic trajectory obtained for n = 0 (A). c–e, A few statistical properties of the DM-1c signals generated at the four backward steps A–D: PDF of δ_τV_i for τ = τ_η (c), second-order structure function, $S_{\tau }^{\left(2\right)}$ (d), fourth-order flatness, $F_{\tau }^{\left(4\right)}$ (e). f, Illustration of one trajectory generation from D to A, corresponding to b. Source data

Fig. 4. Multiscale statistical properties of velocity increments.

a, log–log plot of Lagrangian structure functions, $S_{\tau }^{\left(p\right)}$, for p = 2, 4 and 6, compared across DNS, DM-1c and DM-3c. b, log–log plot of the generalized flatness, $F_{\tau }^{\left(p\right)}$, for p = 4, 6 and 8, compared across DNS, DM-1c and DM-3c. c, log–log plot of fourth-order mixed flatness, $F_{\tau }^{\left(4,ij\right)}$, averaged over combinations of ij = xy, xz and yz for both DNS and DM-3c. The error bars represent the minimum and maximum values obtained for each measure by dividing the entire dataset used to compute the statistics into ten different independent batches of smaller size. Error bars may appear smaller than the data points. Source data

Fig. 5. Scale-by-scale intermittent properties.

a, Comparison between the ground-truth DNS and the two DMs, on the lin-log scale, for the fourth-order logarithmic local slope ζ(4, τ) defined in equation (4). b, The same quantity shown in a from a state-of-the-art collection of DNS^– and experimental data^,,,. The dotted horizontal lines represent the non-intermittent dimensional scaling, $S_{\tau }^{\left(4\right)}\propto \left[S_{\tau }^{\left(2\right)}\right]{}^2$. Statistics and error bars in a are derived as in Fig. 4. This resulted in 30 batches for DNS and DM-3c and ten batches for DM-1c. The error bars in panel b are computed solely over the three different velocity components. Source data

Fig. 6. DM training protocol.

The training loss function, $⟨L_n^{\mathrm{simple}}⟩$, against iterations for DM-1c. Here, 〈 ⋅ 〉 represents the average over a batch of training data, each of which has a corresponding random step n with 0 ≤ n ≤ N. The inset presents the fourth-order flatness obtained from DM-1c at different iterations (A: 10 × 10³, B: 30 × 10³ C: 250 × 10³), in comparison with that from DNS data. Statistics and error bars are derived as in Fig. 4. Source data