Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 May 27;10(4):1019-1036.
doi: 10.1016/j.idm.2025.05.009. eCollection 2025 Dec.

The role of spontaneous clearance on fractional analysis of HBV

O Y Oludoun  1 , O Abiodun  2 , B Gbadamosi  2 , J K Oladejo  3 , E I Akinola  1 , O N Emuoyibofarhe  4 , O Adebimpe  2
Affiliations

The role of spontaneous clearance on fractional analysis of HBV

O Y Oludoun et al. Infect Dis Model. .

Abstract

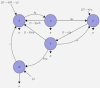
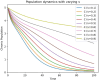
Hepatitis B virus (HBV) remains a persistent global health concern, with recent research advancing our understanding of its transmission dynamics and potential interventions.The present study proposes a mathematical model of Hepatitis B Virus (HBV) epidemics using fractional calculus, with a special emphasis on the influence of spontaneous clearance across diverse population groups. Using the Atangana-Baleanu derivative, the model accounts for the complications of vertical and horizontal transmission, therapy, immunisation, and spontaneous clearance. Numerical simulations with different fractional orders demonstrate how spontaneous clearance affects the dynamics of susceptible, chronic, treated, and recovered populations. The findings indicate that in vulnerable populations, increasing spontaneous clearance reduces vulnerability because people either clear the illness naturally or gain resistance.However, in chronic populations, spontaneous clearance is insufficient for complete recovery without treatment. The combination of therapy and spontaneous clearance improves the treated population, demonstrating the beneficial effects of both medical intervention and natural immunity. Furthermore, increased spontaneous clearance boosts the restored population, demonstrating the immune system's ability to eliminate the virus over time. The fractional-order framework captures the memory effect of illness development, revealing how healing is time-dependent and how immune responses have a long-term impact. This study emphasises the need of combining spontaneous clearance with medical therapies to improve HBV management and public health consequences. Hepatitis B virus (HBV) remains a persistent global health concern, with recent research advancing our understanding of its transmission dynamics and potential interventions. This study presents a fractional mathematical model of HBV infection, employing the Atangana-Baleanu derivative with Mittag-Leffler kernels to capture memory-dependent and nonlocal transmission processes. The model integrates vertical and horizontal transmission pathways, treatment strategies, immunization efforts, and spontaneous clearance, providing a nuanced perspective compared to classical models. Stability conditions are analyzed through fixed-point theory, revealing the global stability of both disease-free and endemic states under specific values of the basic reproduction number R 0. Numerical simulations demonstrate the model's effectiveness in capturing the complex dynamics of HBV, with fractional-order parameters enhancing prediction accuracy. This approach offers valuable insights into optimizing public health interventions and treatment strategies for managing HBV infections effectively.

Keywords: Basic reproduction number; Fixed point theory; Fractal fractional model; Hepatitis B virus; Memory-dependent; Stability.

PubMed Disclaimer

Conflict of interest statement

The authors declare that there are no conflict of interest and funding available for this research

Figures

Fig. 1
Fig. 1
Schematic diagram of mathematical modeling of HBV with vital dynamics.
Fig. 2
Fig. 2
Simulation of the effects of fractional order on Susceptible population of HBV dynamics.
Fig. 3
Fig. 3
Simulation of the effects of fractional order on Chronic population of HBV dynamics.
Fig. 4
Fig. 4
Simulation of the effects of fractional order on Treated population of HBV dynamics.
Fig. 5
Fig. 5
Simulation of the effects of fractional order on Recovered population of HBV dynamics.
See this image and copyright information in PMC

References

    1. Ahmad S., Ullah A., Ali A., Bayatti H.Al. Theoretical analysis of HBV infection under Mittag-Leffler derivative. Progress in Fractional Differentiation and Applications. 2023;9(1):99–106.
    1. Ain Q.T., Chu Y.-M. On fractal fractional hepatitis B epidemic model with modified vaccination effects. Fractals. 2023;31(10) doi: 10.1142/S0218348X23400066. - DOI
    1. Atangana A., Baleanu D. New fractional derivatives with nonlocal and nonsingular kernel: Theory and application to heat transfer model. Thermal Science. 2016;20(2):763–769.
    1. Baleanu D., Diethelm K., Scalas E., Trujillo J.J. Fractional calculus models and numerical methods. World Scientific. Series on Complexity, Nonlinearity and Chaos. 2012;3
    1. Din A., Abidin M.Z. Analysis of fractional-order vaccinated Hepatitis-B epidemic model with Mittag-Leffler kernels. Mathematical Modelling and Numerical Simulation with Applications. 2022;2(2):59–72. doi: 10.53391/mmnsa.2022.006. - DOI

LinkOut - more resources