Run-and-tumble dynamics of Escherichia coli is governed by its mechanical properties

Abstract

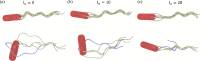
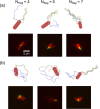
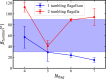
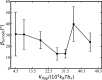
The huge variety of microorganisms motivates fundamental studies of their behaviour with the possibility to construct artificial mimics. A prominent example is the Escherichia coli bacterium, which employs several helical flagella to exhibit a motility pattern that alternates between run (directional swimming) and tumble (change in swimming direction) phases. We establish a detailed E. coli model, coupled to fluid flow described by the dissipative particle dynamics method, and investigate its run-and-tumble behaviour. Different E. coli characteristics, including body geometry, flagella bending rigidity, the number of flagella and their arrangement at the body, are considered. Experiments are also performed to directly compare with the model. Interestingly, in both simulations and experiments, the swimming velocity is nearly independent of the number of flagella. The rigidity of a hook (the short part of a flagellum that connects it directly to the motor), polymorphic transformation (spontaneous change in flagella helicity) of flagella and their arrangement at the body surface strongly influence the run-and-tumble behaviour. Mesoscale hydrodynamics simulations with the developed model help us better understand physical mechanisms that govern E. coli dynamics, yielding the run-and-tumble behaviour that compares well with experimental observations. This model can further be used to explore the behaviour of E. coli and other peritrichous bacteria in more complex realistic environments.

Keywords: bacterium model; hydrodynamic simulation; motility; navigation; propulsion.

Figure 1.

Experimental observation of typical run-and-tumble dynamics of E. coli. Bacterium body is fluorescently labelled in green, while flagella are labelled in red. The run phase is shown in the first and last panels, where all flagella are in a single tight bundle. The tumble phase is illustrated in the remaining panels, where one or several flagella leave the bundle. The scale is the same in all panels and is indicated by the scale bar of 5 µm. See also electronic supplementary material, video S1.

Figure 2.

(a) Escherichia coli model that consists of a sphero-cylinder-like cell body and N_flag = 5 left-handed helical flagella. The hook angle θ_hook is illustrated and defined as the angle between the first section of a flagellum and the body surface. (b) Sphero-cylinder-like cell body described by equation (2.1) has a length of 3 µm and a diameter of 1 µm. It is represented by a collection of $1278$ particles, forming a triangulated spring network on its surface. (c) Model of a left-handed flagellum with three helical turns made of $N_s=76$ segments. It has a diameter of 0.47 µm and a pitch length of 2.56 µm. The flagellum model is adopted from [40].

Figure 3.

Five flagella E. coli model for different values of torque. (a) Average swimming speed $v$ and wobbling angle ${\beta }_w$ as a function of applied torque $T_m$. The swimming speed is computed from a fixed-time displacement and the wobbling angle is defined as the angle between the orientation vector of the body and the axis of flagellar bundle (see the inset at the bottom) during forward swimming (i.e. run phase). The error bars represent s.d. of a number of measurements performed during a run phase of about $1$ s. Insets show snapshots of E. coli for the applied torques ${\displaystyle T_m=100k_{B}T}$ (top) and ${\displaystyle T_m=300k_{B}T}$ (bottom) with a poorly formed and tight flagellar bundle, respectively (see also electronic supplementary material, videos S2 and S3). (b) Rotation frequencies of the body and the bundle as a function of torque. The rotational frequencies are computed over the whole simulation time, where the number of rotations of the body or flagella bundle is divided by the total simulation time.

Figure 4.

Dynamic properties of E. coli with different numbers of flagella (N_flag = 1, 3–7) during the run phase. ${\displaystyle T_m=300k_{B}T}$ in all cases. (a) Swimming speed $v$ and wobbling angle ${\beta }_w$ for a simulated E. coli as a function of the number of flagella (see electronic supplementary material, videos S4 and S5 for N_flag = 1 and N_flag = 7). (b) Simulated rotation frequencies $\omega$ of the body and the bundle for different N_flag. (c) Experimental measurements of E. coli swimming speed near a surface as a function of the flagella number (see §2.4 for practical details).

Figure 5.

Escherichia coli model with a spheroidal body. (a) Dimensions of the body with a spheroidal shape. (b) Illustrative snapshot of a bacterium during tumbling (see also electronic supplementary material, video S6). Here, N_flag = 5, ${\displaystyle K_{\text{flag}}=2.7\times {10}^5{k}_{B}T{b}_x}$, ${\displaystyle K_{\text{hook}}=500k_{B}T}$ and ${\displaystyle T_m=300k_{B}T}$. The reverted flagellum does not undergo polymorphic transformation and hook stiffening.

Figure 6.

Escherichia coli models with a varying length of the linear flagellum section at the attachment to the body. (a) No initial linear section with full three turn left-handed helices. (b) An initial linear section of $l_n=10$ segments ($13\%$ of the contour length). (c) An initial linear section of $l_n=20$ segments ($26\%$ of the contour length). Snapshots in the top row show the run phase, while the bottom row illustrates the tumble phase. In all models, ${\displaystyle N_{\text{flag}}=5}$, ${\displaystyle K_{\text{flag}}=2.7\times {10}^5{k}_{B}T{b}_x}$, ${\displaystyle K_{\text{hook}}=200k_{B}T}$ and ${\displaystyle T_m=300k_{B}T}$. In all three cases, no polymorphic transformation and hook stiffening are incorporated.

Figure 7.

Tumble behaviour of E. coli with polymorphic transformation of the reverted flagellum (see also electronic supplementary material, video S7). Here, ${\displaystyle N_{\text{flag}}=5}$, ${\displaystyle K_{\text{flag}}=2.7\times {10}^5{k}_{B}T{b}_x}$, ${\displaystyle K_{\text{hook}}=200k_{B}T}$ and ${\displaystyle T_m=300k_{B}T}$. Hook stiffening is not incorporated.

Figure 8.

Tumble behaviour of E. coli models with different hook rigidities. (a) All flagella have a flexible hook with K_hook = 0. (b) All flagella with ${\displaystyle K_{\text{hook}}=100k_{B}T}$. (c) All flagella possess ${\displaystyle K_{\text{hook}}=200k_{B}T}$. (d) All flagella have a hook rigidity of ${\displaystyle 500k_{B}T}$. (e) A model where the reverted flagellum has ${\displaystyle K_{\text{hook}}=500k_{B}T}$, while the other flagella possess a hook rigidity of $100k_{B}T$ (see also electronic supplementary material, video S8). In all cases, the polymorphic transformation of the clockwise-rotating flagellum is implemented. Here, ${\displaystyle N_{\text{flag}}=5}$, ${\displaystyle K_{\text{flag}}=2.7\times {10}^5{k}_{B}T{b}_x}$ and ${\displaystyle T_m=300k_{B}T}$.

Figure 9.

Escherichia coli models with different arrangements of flagella in comparison to experiments. (a) A symmetrical arrangement of flagella with one flagellum attached at the back along the body axis and the other four attached symmetrically at the body circumference with a ${90}^{\circ }$ separation. In the experiment, the flagella are primarily located near one end of the body. See also electronic supplementary material, videos S8 and S10. (b) Random distribution of flagella attachment points on the whole body (see electronic supplementary material, videos S9 and S11). Snapshots in the top row show the run phase, while the bottom row illustrates the tumble phase. In simulations, ${\displaystyle N_{\text{flag}}=5}$, ${\displaystyle K_{\text{flag}}=2.7\times {10}^5{k}_{B}T{b}_x}$, ${\displaystyle T_m=300k_{B}T}$ and the hook rigidity of the reverted flagellum is ${\displaystyle 500k_{B}T}$ with polymorphic transformation, while the other flagella have ${\displaystyle K_{\text{hook}}=100k_{B}T}$. The scale is the same in all experimental panels and is indicated by the scale bar of 5 µm.

Figure 10.

Tumble phase of E. coli models with different numbers of flagella. Snapshots of several cases with (a) one reverted flagellum and (b) two reverted flagella. For comparison, several experimental snapshots are also included next to the simulation snapshots. Note that N_flag values should be considered only for the simulation snapshots, as in the experimental observations, it is not possible to count the number of flagella. See also electronic supplementary material, videos S8 and S12–S16. In all simulations, ${\displaystyle K_{\text{flag}}=2.7\times {10}^5{k}_{B}T{b}_x}$, ${\displaystyle T_m=300k_{B}T}$ and the hook rigidity of the reverted flagellum is ${\displaystyle 500k_{B}T}$ with polymorphic transformation, while the other flagella have ${\displaystyle K_{\text{hook}}=100k_{B}T}$. The scale is the same in all experimental panels and is indicated by the scale bar of 5 µm.

Figure 11.

Tumble angles β_tumble of E. coli with different numbers of flagella (see snapshots in figure 10). The data are obtained from simulations with a symmetrical arrangement of flagella with one flagellum attached at the back along the body axis and the others attached symmetrically at the body circumference. The blue curve represents cases with one reverted flagellum, and the red curve corresponds to simulations with two reverted flagella. The blue shade indicates the range of tumble angles measured experimentally [11]. The tumble angle is defined as the angle between the orientation vector of the body before and after a tumble event. The error bars represent s.d.

Figure 12.

Tumble angle β_tumble of E. coli as a function of flagella bending stiffness. Here, only one reverted flagellum is employed with N_flag = 5. The tumble angle is defined as the angle between the orientation vector of the body before and after a tumble event. Each data point is averaged over three tumble events.