Crossover operators for molecular graphs with an application to virtual drug screening
- PMID: 40528251
- PMCID: PMC12175394
- DOI: 10.1186/s13321-025-00958-w
Crossover operators for molecular graphs with an application to virtual drug screening
Abstract
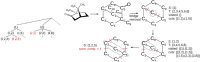
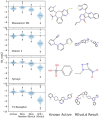
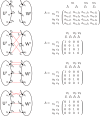
Genetic algorithms are a powerful method to solve optimization problems with complex cost functions over vast search spaces that rely in particular on recombining parts of previous solutions. Crossover operators play a crucial role in this context. Here, we describe a large class of these operators designed for searching over spaces of graphs. These operators are based on introducing small cuts into graphs and rejoining the resulting induced subgraphs of two parents. This form of cut-and-join crossover can be restricted in a consistent way to preserve local properties such as vertex-degrees (valency), or bond-orders, as well as global properties such as graph-theoretic planarity. In contrast to crossover on strings, cut-and-join crossover on graphs is powerful enough to ergodically explore chemical space even in the absence of mutation operators. Extensive benchmarking shows that the offspring of molecular graphs are again plausible molecules with high probability, while at the same time crossover drastically increases the diversity compared to initial molecule libraries. Moreover, desirable properties such as favorable indices of synthesizability are preserved with sufficient frequency that candidate offsprings can be filtered efficiently for such properties. As an application we utilized the cut-and-join crossover in REvoLd, a GA-based system for computer-aided drug design. In optimization runs searching for ligands binding to four different target proteins we consistently found candidate molecules with binding constants exceeding the best known binders as well as candidates found in make-on-demand libraries.Scientific contributionWe define cut-and-join crossover operators on a variety of graph classes including molecular graphs. This constitutes a mathematically simple and well-characterized approach to recombination of molecules that performed very well in real-life CADD tasks.
Keywords: Crossover; Genetic algorithm; Graph theory; Virtual screening.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare no Competing interests.
Figures

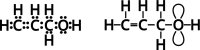

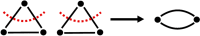


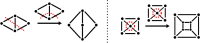


Similar articles
-
Restless reachability problems in temporal graphs.Knowl Inf Syst. 2025;67(7):5651-5697. doi: 10.1007/s10115-025-02405-6. Epub 2025 Apr 1. Knowl Inf Syst. 2025. PMID: 40535024 Free PMC article.
-
Assessing the comparative effects of interventions in COPD: a tutorial on network meta-analysis for clinicians.Respir Res. 2024 Dec 21;25(1):438. doi: 10.1186/s12931-024-03056-x. Respir Res. 2024. PMID: 39709425 Free PMC article. Review.
-
Prediction, screening and characterization of novel bioactive tetrapeptide matrikines for skin rejuvenation.Br J Dermatol. 2024 Jun 20;191(1):92-106. doi: 10.1093/bjd/ljae061. Br J Dermatol. 2024. PMID: 38375775
-
Defining disease severity in atopic dermatitis and psoriasis for the application to biomarker research: an interdisciplinary perspective.Br J Dermatol. 2024 Jun 20;191(1):14-23. doi: 10.1093/bjd/ljae080. Br J Dermatol. 2024. PMID: 38419411 Free PMC article. Review.
-
Platelet Indices and RDW to Assess Inflammatory Milieu in Subclinical Hashimoto's Thyroiditis.Clin Med Insights Endocrinol Diabetes. 2025 Jun 13;18:11795514251349337. doi: 10.1177/11795514251349337. eCollection 2025. Clin Med Insights Endocrinol Diabetes. 2025. PMID: 40528863 Free PMC article.
References
-
- Cayley A (1874) On the mathematical theory of isomers. Phil Mag 47:444–446
-
- Estrada E (2011) The Structure of Complex Networks: Theory and Applications. Oxford University Press, Oxford, UK
-
- Khan IH (2015) Assessing different crossover operators for Travelling Salesman Problem. Intl J Intelligent Systems and Applications 11:19–25. 10.5815/ijisa.2015.11.03
-
- McInnes C (2007) Virtual screening strategies in drug discovery. Current Opinion in Chemical Biology 11(5):494–502. 10.1016/j.cbpa.2007.08.033 - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

