Quadratic mixed convection of Maxwell-Buongiorno nanofluid over cubic stratified surface incorporating cross diffusion effects and solar radiation
- PMID: 40542170
- PMCID: PMC12181417
- DOI: 10.1038/s41598-025-07140-0
Quadratic mixed convection of Maxwell-Buongiorno nanofluid over cubic stratified surface incorporating cross diffusion effects and solar radiation
Abstract
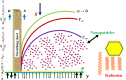
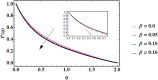
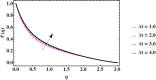
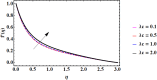
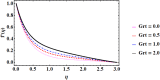
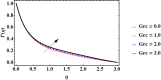
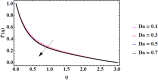
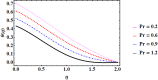
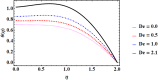
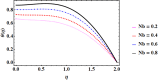
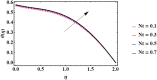
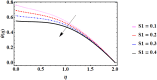
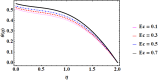
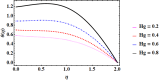
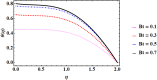
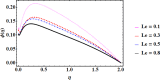
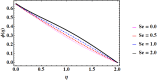
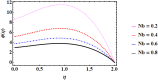
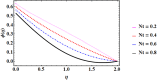
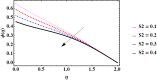
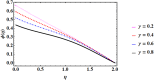
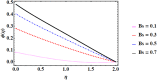
Cubic stratification dramatically enhances thermal and mass transport in quadratic mixed convection, which is advantageous for electronics cooling, biomedical technology, and power plants. Nanofluids are essential to the development of next-generation cooling and environmental management solutions because of their exceptional thermal characteristics. Motivated by such impactful applications in thermal and engineering systems, this work uses the Buongiorno model to examine heat and mass transfer in Maxwell nanofluids over a vertically extended permeable surface under Darcy-Forchheimer porous flow situations. For a more accurate depiction, convective boundary conditions and suction-injection effects are also included in the current analysis. In order to represent complete heat and mass transport behavior, the model also takes into consideration radiative heat flux, viscous heating, chemical reaction, and cross-diffusion effects through the Soret and Dufour mechanisms. Similarity transformations are used to convert the controlling partial differential equations into a system of ordinary differential equations, which are then numerically solved using Mathematica's NDSolve approach. The influence of important physical parameters on thermal profiles, fluid velocity fields, and concentration distribution is demonstrated in detail through a visual analysis. The skin friction coefficient and local Nusselt and Sherwood numbers are calculated and studied in detail to determine the rates of heat, mass, and surface drag. Important key findings shows that the Velocity filed upsurges with nonlinear thermal and convection parameters, whereas it declines with higher Darcy and Forchheimer resistance effects. Moreover, nanofluid temperature is increased by Dufour and Eckert numbers and decreased by thermal stratification parameter. Finally, Soret and solutal Biot numbers enhance nanoparticle concentration, whereas solutal stratification parameter diminishes it. The results exhibit outstanding consistency with previous research published in the literature.
Keywords: Convective boundary conditions; Cross diffusion phenomena; Cubic stratification; Maxwell nanofluid; Nonlinear convection; Solar radiation.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare no competing interests.
Figures
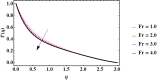
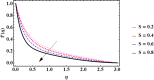
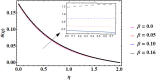
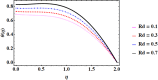
Similar articles
-
Computational insights into silver oxide nanoparticles on flow and Cattaneo-Christov heat flux through a Koo and Kleinstreuer model: A heat transfer application.Sci Rep. 2025 Aug 4;15(1):28427. doi: 10.1038/s41598-025-13753-2. Sci Rep. 2025. PMID: 40760007 Free PMC article.
-
Response surface optimization for Minsta-Gherasim hybrid nanofluid flow over a porous surface with varying water temperature levels and magnetic influence.Sci Rep. 2025 Aug 19;15(1):30375. doi: 10.1038/s41598-025-14633-5. Sci Rep. 2025. PMID: 40830386 Free PMC article.
-
Effects of variable heat rise/fall on MHD Maxwell ternary nanofluid (Copper-Alumina-Titanium Dioxide/Water) flow over a moving needle.Sci Rep. 2025 Jul 12;15(1):25209. doi: 10.1038/s41598-025-10057-3. Sci Rep. 2025. PMID: 40652007 Free PMC article.
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
-
A rapid and systematic review of the clinical effectiveness and cost-effectiveness of paclitaxel, docetaxel, gemcitabine and vinorelbine in non-small-cell lung cancer.Health Technol Assess. 2001;5(32):1-195. doi: 10.3310/hta5320. Health Technol Assess. 2001. PMID: 12065068
References
-
- Choi, S. U. S. Nanofluid Technology: Current Status and Future Research (Argonne National Lab.(ANL), 1998). Argonne, IL (United States).
-
- Buongiorno, J. Convective transport in nanofluids (2006).
-
- Reza-E-Rabbi, S., Ahmmed, S. F., Arifuzzaman, S., Sarkar, T. & Khan, M. S. Computational modelling of multiphase fluid flow behaviour over a stretching sheet in the presence of nanoparticles. Eng. Sci. Technol. Int. J.23 (3), 605–617 (2020).
-
- Reza-E-Rabbi, S., Arifuzzaman, S., Sarkar, T., Khan, M. S. & Ahmmed, S. F. Explicit finite difference analysis of an unsteady MHD flow of a chemically reacting Casson fluid past a stretching sheet with brownian motion and thermophoresis effects. J. King Saud Univ. -Sci. 32 (1), 690–701 (2020).
-
- Ratha, P. K., Mishra, S., Tripathy, R. & Pattnaik, P. K. Analytical approach on the free convection of Buongiorno model nanofluid over a shrinking surface, Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst.. 237(3–4), 83–95 (2023).
LinkOut - more resources
Full Text Sources