A Novel Exploration Stage Approach to Improve Crayfish Optimization Algorithm: Solution to Real-World Engineering Design Problems

Abstract

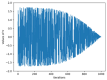
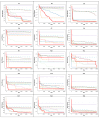
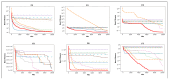
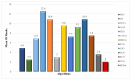
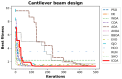
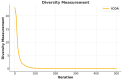
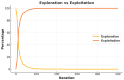
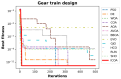
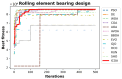
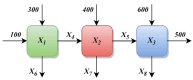
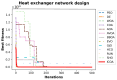
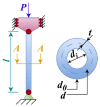
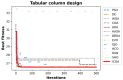
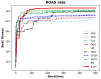
The Crayfish Optimization Algorithm (COA) has limitations that affect its optimization performance seriously. The competition stage of the COA uses a simplified mathematical model that concentrates on relations of distance between crayfish only. It is deprived of a stochastic variable and is not able to generate an applicable balance between exploration and exploitation. Such a case causes the COA to have early convergence, to perform poorly in high-dimensional problems, and to be trapped by local minima. Moreover, the low activation probability of the summer resort stage decreases the exploration ability more and slows down the speed of convergence. In order to compensate these shortcomings, this study proposes an Improved Crayfish Optimization Algorithm (ICOA) that designs the competition stage with three modifications: (1) adaptive step length mechanism inversely proportional to the number of iterations, which enables exploration in early iterations and exploitation in later stages, (2) vector mapping that increases stochastic behavior and improves efficiency in high-dimensional spaces, (3) removing the X_shade parameter in order to abstain from early convergence. The proposed ICOA is compared to 12 recent meta-heuristic algorithms by using the CEC-2014 benchmark set (30 functions, 10 and 30 dimensions), five engineering design problems, and a real-world ROAS optimization case. Wilcoxon Signed-Rank Test, t-test, and Friedman rank indicate the high performance of the ICOA as it solves 24 of the 30 benchmark functions successfully. In engineering applications, the ICOA achieved an optimal weight (1.339965 kg) in cantilever beam design, a maximum load capacity (85,547.81 N) in rolling element bearing design, and the highest performance (144.601) in ROAS optimization. The superior performance of the ICOA compared to the COA is proven by the following quantitative data: 0.0007% weight reduction in cantilevers design (from 1.339974 kg to 1.339965 kg), 0.09% load capacity increase in bearing design (COA: 84,196.96 N, ICOA: 85,498.38 N average), 0.27% performance improvement in ROAS problem (COA: 144.072, ICOA: 144.601), and most importantly, there seems to be an overall performance improvement as the COA has a 4.13 average rank while the ICOA has 1.70 on CEC-2014 benchmark tests. Results indicate that the improved COA enhances exploration and successfully solves challenging problems, demonstrating its effectiveness in various optimization scenarios.

Keywords: crayfish optimization; engineering design problems; meta-heuristic algorithm; swarm intelligence.

Figure 1

Research flow diagram.

Figure 2

Dynamic behavior of V.

Figure 3

Results of some algorithms for CEC-2014 (D = 10).

Figure 3

Results of some algorithms for CEC-2014 (D = 10).

Figure 3

Results of some algorithms for CEC-2014 (D = 10).

Figure 4

Results of some algorithms for CEC-2014 (D = 30).

Figure 4

Results of some algorithms for CEC-2014 (D = 30).

Figure 5

Convergence curves of ICOA and competing algorithms for CEC-2014 (D = 10).

Figure 5

Convergence curves of ICOA and competing algorithms for CEC-2014 (D = 10).

Figure 6

Convergence curves of ICOA and competing algorithms for CEC-2014 (D = 30).

Figure 6

Convergence curves of ICOA and competing algorithms for CEC-2014 (D = 30).

Figure 6

Convergence curves of ICOA and competing algorithms for CEC-2014 (D = 30).

Figure 7

The average ranks of algorithms in different dimensions.

Figure 8

Cantilever beam design problem.

Figure 9

Convergence curves of ICOA and competing algorithms for cantilever beam design.

Figure 10

Population diversity of ICOA for cantilever beam design.

Figure 11

Exploration–exploitation balance of ICOA for cantilever beam design.

Figure 12

Gear train design problem.

Figure 13

Convergence curves of ICOA and competing algorithms for gear train design.

Figure 14

Rolling element bearing design problem.

Figure 15

Convergence curves of ICOA and competing algorithms for rolling element bearing design.

Figure 16

Heat exchanger network design problem.

Figure 17

Convergence curves of ICOA and competing algorithms for heat exchanger network design.

Figure 18

Tabular column design problem.

Figure 19

Convergence curves of ICOA and competing algorithms for tabular column design.

Figure 20

Convergence curves of ICOA and competing algorithms for ROAS problem.