Sign-Entropy Regularization for Personalized Federated Learning

Abstract

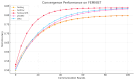
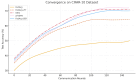
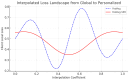
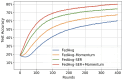
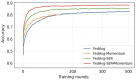
Personalized Federated Learning (PFL) seeks to train client-specific models across distributed data silos with heterogeneous distributions. We introduce Sign-Entropy Regularization (SER), a novel entropy-based regularization technique that penalizes excessive directional variability in client-local optimization. Motivated by Descartes' Rule of Signs, we hypothesize that frequent sign changes in gradient trajectories reflect complexity in the local loss landscape. By minimizing the entropy of gradient sign patterns during local updates, SER encourages smoother optimization paths, improves convergence stability, and enhances personalization. We formally define a differentiable sign-entropy objective over the gradient sign distribution and integrate it into standard federated optimization frameworks, including FedAvg and FedProx. The regularizer is computed efficiently and applied post hoc per local round. Extensive experiments on three benchmark datasets (FEMNIST, Shakespeare, and CIFAR-10) show that SER improves both average and worst-case client accuracy, reduces variance across clients, accelerates convergence, and smooths the local loss surface as measured by Hessian trace and spectral norm. We also present a sensitivity analysis of the regularization strength ρ and discuss the potential for client-adaptive variants. Comparative evaluations against state-of-the-art methods (e.g., Ditto, pFedMe, momentum-based variants, Entropy-SGD) highlight that SER introduces an orthogonal and scalable mechanism for personalization. Theoretically, we frame SER as an information-theoretic and geometric regularizer that stabilizes learning dynamics without requiring dual-model structures or communication modifications. This work opens avenues for trajectory-based regularization and hybrid entropy-guided optimization in federated and resource-constrained learning settings.

Keywords: entropy regularization; federated learning; gradient sign patterns; personalization; polynomial root geometry.

Figure 1

Convergence curves (test accuracy vs. communication rounds) on FEMNIST, Shakespeare, and CIFAR-10. SER-enhanced methods show faster and more stable convergence compared to baselines. Shaded regions show the standard deviation over three runs.

Figure 2

Convergence curves on the Shakespeare dataset for FedAvg, FedAvg-SER, Ditto, and pFedMe. FedAvg-SER and Ditto converge faster and more stably than FedAvg, with Ditto achieving the highest final accuracy. pFedMe converges more slowly, but reaches comparable final performance.

Figure 3

Convergence curves on the CIFAR-10 dataset for FedAvg, FedAvg+FT, FedAvg-SER, Ditto, and pFedMe. FedAvg-SER and Ditto show faster and more stable convergence than FedAvg, with pFedMe ultimately achieving the highest accuracy. All methods were averaged over three runs, with standard deviations omitted for clarity.

Figure 4

Gradient sign entropy dynamics: (a) mean entropy across all clients over training rounds and (b) individual entropy trajectories for two clients with distinct data distributions. SER consistently reduces entropy, indicating smoother optimization paths.

Figure 5

Interpolated loss curves between global and personalized models for a sample client. The SER-regularized loss exhibits a smoother unimodal shape, supporting the hypothesis that SER encourages flatter regions of the loss landscape.

Figure 6

Convergence on CIFAR-10 comparing FedAvg, FedAvg-Momentum, FedAvg-SER, and FedAvg-SER+Momentum.

Figure 7

Convergence on FEMNIST comparing FedAvg, FedAvg-Momentum, FedAvg-SER, and FedAvg-SER+Momentum.