Exploring Numerical Correlations: Models and Thermodynamic Kappa

Abstract

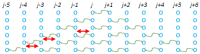
McComas et al. (2025) introduced a numerical experiment, where ordinary uncorrelated collisions between collision pairs are followed by other, controlled (correlated) collisions, shedding light on the emergence of kappa distributions through particle correlations in space plasmas. We extend this experiment by introducing correlations indicating that (i) when long-range correlations are interwoven with collision pairs, the resulting thermodynamic kappa are described as that corresponding to an 'interatomic' potential interaction among particles; (ii) searching for a closer description of heliospheric plasmas, we found that pairwise short-range correlations are sufficient to lead to appropriate values of thermodynamic kappa, especially when forming correlated clusters; (iii) multi-particle correlations do not lead to physical stationary states; finally, (iv) an optimal model arises when combining all previous findings. In an excellent match with space plasmas observations, the thermodynamic kappa that describes the stationary state at which the system is stabilized behaves as follows: (a) When correlations are turned off, kappa is turning toward infinity, indicating the state of classical thermal equilibrium (Maxwell-Boltzmann distribution), (b) When collisions are turned off, kappa is turning toward the anti-equilibrium state, the furthest state from the classical thermal equilibrium (-5 power-law phase-space distribution), and (c) the finite kappa values are generally determined by the competing factor of collisions and correlations.

Keywords: correlations; heliosphere; kappa distributions; numerical experiment; solar wind; space plasmas.

Figure 1

The original model suggested by McComas et al. [18]. In the first step a collision takes place between the i and the $i+1$ particle as shown by the double headed red arrow, while at the second time step “pseudo-collision”, or controlled collision, occurs between the randomly selected particle j and its adjacent particle $j+1$ (shown by the curly green line with arrowheads). McComas et al. [18] also allowed the repetition of the controlled collision step $M-1(>0)$ times where each time we randomly select the position of the j particle. The model is complimented by periodic boundary conditions that means the particle next to the $i=i_{max}=N$ particle is the one at $i=1$.

Figure 2

Results obtained from the original model of McComas et al. [18] for the case $f=0.95$ and $M=1$. Here, $N={10}^6$ particles are used for $\tau =3\times {10}^5$ MCS. The results of 12 replicas obtained through different initial conditions, due to different random number generator seeds, have been merged to improve the statistics. In the upper panel, we show the complementary cumulative distribution function $F_{ccd}\left(E\right)$, as in [18], while in the lower panel the pdf $f\left(E\right)$ is plotted; in the figure key the symbol “$\ast \ast$” stands for exponentiation. The value of ${\kappa }_0$ obtained through Equation (20) is ${\kappa }_0=13.5\pm 0.3$.

Figure 3

Two equivalent models in which during the second time step the “pseudo-collision”, or controlled collision, occurs between one particle of the CP (linked with the red double headed arrow) that collided during the first time step and its nearest neighbor (shown by the curly green line with arrowheads).

Figure 4

Results obtained from the two models of Figure 3 for the case $f=0.95$. Here, $N={10}^6$ particles with $\tau =3\times {10}^5$ MCS. In the upper panel, we show the complementary cumulative distribution function $F_{ccd}\left(E\right)$ with blue plus symbols for the model in upper panel of Figure 3 and red continuous line for the one in the lower panel of Figure 3; in the figure key the symbol “$\ast \ast$” stands for exponentiation. The lower panel depicts the two pdfs $f\left(E\right)$ for the model in the upper and lower panel of Figure 3 with plus symbols and open circles, respectively. The green lines correspond to the simultaneous fit by kappa distributions of Equations (13) and (19) and leads through Equation (20) to a value of ${\kappa }_0=21.5\pm 0.3$.

Figure 5

The two models of varying long-range correlations at a distance R that have been studied in Section 2.2.2. From top to bottom and for the class of the models shown in panel (A) $R=1, 2, 3,$ and 6 while for those shown in (B) we set $R=1, 2,$ and 5. In all cases, the CP is at the particles j and $j+1$ and is indicated by the red double headed arrow.

Figure 6

Results of models“a” (blue) and “b” (red) for ${\kappa }_0$ vs. the range R used in the correlation step (see Figure 5), plotted on linear-linear and linear-log scales; in the figure key the symbol “$\ast \ast$” stands for exponentiation. The continuous lines in each case have been drawn as a guide to the eye. The thick horizontal black line indicates the value of ${\kappa }_0$ estimated in Figure 2 while the thinner black lines the corresponding error.

Figure 7

Results of the “lr” model discussed in Section 2.2.3: ${\kappa }_0$ vs the range m as estimated by fitting $F_{ccd}\left(E\right)$ in the energy range $E\in [1.5,15]$ to the distribution of energies obtained by at least 10 replicas of $N={10}^6$ particles in each case. The continuous green line has been drawn as a guide to the eye. The ${\kappa }_0$ value at $m=1$ corresponds that estimated in Figure 2.

Figure 8

Class of models “m” in which the “donor” particle at j gives a part f of its energy to its six nearest neighbors $j-3$, $j-2$, $j-1$, $j+1$, $j+2$, $j+3$ with percentages $r_{-3}$, $r_{-2}$, $r_{-1}$, $r_1$, $r_2$, and $r_3$, respectively, after the collision step at the CP i and $i+1$.

Figure 9

Results obtained from various models “m” with different distribution $r_s$ (shown in the legend) of the energy of the donor particle at j to its neighbors (see Figure 8) for the case $f=0.95$. Here, $N={10}^6$ particles have been considered for $\tau =3\times {10}^5$ MCS and the results of 24 replicas obtained through different initial conditions due to different random number generator seeds have been merged to improve the statistics. In the upper panel, we show the complementary cumulative distribution function $F_{ccd}\left(E\right)$, while in the lower panel the pdf $f\left(E\right)$ is plotted. The continuous curves in the lower panel are parabolas showing that “m” models do not lead to kappa distributions but rather to Gaussians.

Figure 10

A class of models, labeled C1 to C7 according to the number of correlation time steps followed from top to bottom, where after the collision at the CP, we attempt to form a correlated cluster by simultaneously pseudo-colliding the particles around the j and $j+1$ pair. Each curly green line indicates a pseudo-collision and the number of steps increases by one each time we move down the rows that form the edges of the pyramid structure.

Figure 11

Results obtained from model C7, i.e., the whole model depicted in Figure 10 with seven correlation time steps for the case $f=0.95$. Here, $N={10}^6$ particles have been considered for $\tau =3\times {10}^5$ MCS and the results of 24 replicas obtained through different initial conditions due to different random number generator seeds have been merged to improve the statistics. In the upper panel, we show the complementary cumulative distribution function $F_{ccd}\left(E\right)$, while in the lower panel the pdf $f\left(E\right)$ is plotted; in the figure key the symbol “$\ast \ast$” stands for exponentiation. The continuous curves in both panels show the simultaneous fits for both the ccd and the pdf with ${\kappa }_0=5.8\pm 0.3$.

Figure 12

By adding ordinary collisions (denoted by the red double headed arrows) between the steps of the C# class models, we limit the effect of the correlation cluster. These models are labeled as C4-t1 for the model with 4 correlation time steps and one ordinary collision, C5-t2 for the model with 5 correlation time steps and two ordinary collisions, and C6-t3 for the model with 6 correlation time steps and 3 ordinary collisions that corresponds to the totality of the figure.

Figure 13

Results obtained from models C6-t3, i.e., the model depicted in Figure 12 for the case $f=0.95$, and C3. Here, $N={10}^6$ particles have been considered for $\tau =3\times {10}^5$ MCS and the results of 24 replicas obtained through different initial conditions due to different random number generator seeds have been merged to improve the statistics. As mentioned in the text, we also include the results obtained from the model C3 of Figure 10, in which we consider only three correlation time steps, that give rise to curves which are higher than those of the C6-t3 model pointing to stronger correlation and smaller ${\kappa }_0$. In the upper panel, we show the complementary cumulative distribution function $F_{ccd}\left(E\right)$, while in the lower panel the pdf $f\left(E\right)$ is plotted; in the figure key the symbol “$\ast \ast$” stands for exponentiation. The continuous curves in both panels show the simultaneous fits for both the ccd and the pdf of C6-t3 with ${\kappa }_0=8.2\pm 0.3$.

Figure 14

Results obtained for the energy distribution of adjacent particles i and $i+1$ when (A) only the collision step is involved in the calculation, i.e., the upper line of Figure 1, (B) after $\tau =3\times {10}^5$ MCS for the model with $M=2$ and $f=0.95$ (results of which were presented in Figure 2 of McComas et al. [18]), and (C) after $\tau =3\times {10}^5$ MCS with only collision steps but starting from the distribution shown in (B). Here, we show the distribution of $E_i$ and $E_{i+1}$ by simply depicting the points ($E_i$, $E_{i+1}$) as dots (forming a cloud) and $N={10}^6$ particles.

Figure 15

The same as Figure 14 but on an expanded scale where we depict the distribution of Figure 14A (blue dots) on top of the distribution of Figure 14B (red dots).

Figure 16

Here we consider $N={10}^6$, $f=0.95$ and only controlled collisions take place starting from a MB distribution for the energies, see, e.g., Figure 14A. After $\tau =3\times {10}^5$ MCS we have: (A) The energy distribution of adjacent particles i and $i+1$, (B) the complementary cumulative distribution function $F_{ccd}\left(E\right)$, and (C) the pdf $f\left(E\right)$. The continuous curves in the lower two panels show the simultaneous fits for both the ccd and the pdf with ${\kappa }_0=2.5\pm 0.3$.

Figure 17

The values of ${\kappa }_0$ obtained from various models of Figure 10 and Figure 12 that include a correlated cluster versus f. As we increase the number of correlation time steps, correlation increases and ${\kappa }_0$ approaches 0. The introduction of ordinary collisions frustrates the correlated cluster and effectively cancel the correlation steps.