Mean-field and Fluctuations for Hub Dynamics in Heterogeneous Random Networks

Abstract

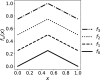
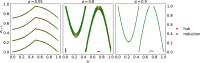
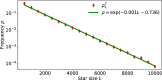
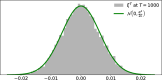
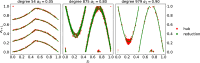
We study a class of heterogeneous random networks, where the network degree distribution follows a power-law, and each node dynamics is a random dynamical system, interacting with neighboring nodes via a random coupling function. We characterize the hub behavior by the mean-field, subject to statistically controlled fluctuations. In particular, we prove that the fluctuations are small over exponentially long time scales and obtain Berry-Esseen estimates for the fluctuation statistics at any fixed time. Our results provide an explanation for several numerical observations, namely, a scaling relation between system size and frequency of large fluctuations, the system size induced desynchronization, and the Gaussian behavior of the fluctuations.

Fig. 1

Graphs of four contractions $f_{\omega }$, $\omega =0,1,2,3$ on the circle $\mathbb{T}=[0,1]/0\sim 1$

Fig. 2

Numerical simulations for the star network dynamics (4) on $N={10}^6$ nodes at various coupling strengths $\alpha =0.05,0.8,0.9$ on the left, center and right panels respectively, with iid random iteration of four circle contractions (2) as isolated node dynamics and (3) as pairwise interaction. The plots show the return behaviors of the hub, that is, the states $z^t$ on horizontal axis against the next states $z^{t+1}$ on vertical axis. Novel hub behaviors emerge from network interactions and vary across different coupling strengths: uniform contraction, expanding region and deterministic fixed point. The mean-field dimensional reduction ansatz yields a reduced one-dimensional system, whose graph, plotted in green, fits very well the actual hub behavior in red

Fig. 3

Frequency of large fluctuations decreases exponentially in system size. The red diamonds mark the frequency ${\rho }_{\epsilon }^T$ up to time $T=2\times {10}^5$ of large mean-field fluctuations, i.e., $|{\xi }^t|>\epsilon$ with threshold $\epsilon =0.025$. The horizontal axis for system size L is in linear scale, whereas the vertical axis for frequency ${\rho }_{\epsilon }^T$ is in logarithmic scale. The green line provides a tight linear fit, indicating an exponential decrease of ${\rho }_{\epsilon }^T$ in L

Fig. 4

Gaussian fluctuations. The grey histogram presents the fluctuations data ${\{{\xi }_n^T\}}_{n=1}^4$ corresponding to ${10}^4$ independent trials of network initial conditions; each ${\xi }_n^T$ is obtained by starting at initial condition trial n and iterating for $T=1000$ times the network dynamics at coupling strength $\alpha =0.9$ on the star of size $L={10}^4$. The green curve shows the probability density function of the normal distribution $\mathcal{N}(0,\frac{{\alpha }^2}{2L})$ with zero mean and variance $\frac{{\alpha }^2}{2L}$. The tight fit indicates that the fluctuation ${\xi }^T$ at time $T=1000$ has Gaussian statistics

Fig. 5

Random power-law network $G_1$ generated from Chung-Lu model on $N=998168$ nodes with power-law exponent $\beta =3$, largest degree ${\mathrm{\Delta }}_0=979$ and lowest degree 1. The left panel shows in log-log scale the degree distribution of $G_1$, that is, degree k in horizontal axis versus the frequency P(k) of nodes of degree k. The power-law in green highlights the fact that $P(k)\propto k^{-3}$. The right panel draws the subgraph S of $G_1$ restricted to three nodes of degrees 54, 875, 979, shown in the center, together with their neighbors in $G_1$ shown as surrounding, with node degrees reflected by size and color. This indicates that most neighbors of a hub in $G_1$ are of low degree

Fig. 6

Hub dynamics of various effective coupling strengths. On power-law network $G_1$ with maximum degree ${\mathrm{\Delta }}_0=979$, we run dynamics (1) at fixed coupling strength $\alpha =0.9$. The left, center, right panels concern three nodes of degree 54, 875, 979 respectively; each panel presents in red the node state $z^t$ versus next state $z^{t+1}$. The three nodes experience the mean-field dimensional reduction of effective coupling strengths ${\alpha }_i$ proportional to their degrees, plotted in green

Fig. 7

System size induced desynchronization between the two most massive hubs on a power-law network. We simulate the $G_1$-network dynamics on $N=99816$ nodes at coupling strength $\alpha =0.9$, and plot in grey the time series of hub desynchronization level ${\eta }^t:=z_{i_0}^t-z_{i_1}^t$ between hubs $i_0$ of degree ${\mathrm{\Delta }}_0=979$ and $i_1$ of degree 978. Large ${\eta }^t$ indicate desynchronization episodes. The green time series shows comparatively small fluctuations ${\xi }_{i_0}^t$, with the green shaded band indicating the trapping region $[z_{-},z_{+}]$ of the reduced dynamics $f_{0.9}$ re-centered at fixed point $z_{\ast }^{}=f_{0.9}z_{\ast }^{}$. The inset highlights the desynchronization mechanism, namely, an instance of a fluctuation ${\xi }_{i_0}^t$ sufficiently large to kick the hub $z_{i_0}^t$ out of the trapping region $[z_{-},z_{+}]$ causes a subsequent episode of desynchronization