Harmonic oscillator based particle swarm optimization
- PMID: 40577322
- PMCID: PMC12204584
- DOI: 10.1371/journal.pone.0326173
Harmonic oscillator based particle swarm optimization
Abstract
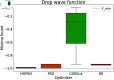
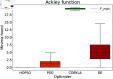
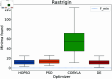
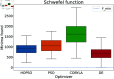
Numerical optimization techniques are widely applied across various fields of science and technology, ranging from determining the minimal energy of systems in physics and chemistry to identifying optimal routes in logistics or strategies for high-speed trading. Here, we present a novel method that integrates particle swarm optimization (PSO), a highly effective and widely used algorithm inspired by the collective behavior of bird flocks searching for food, with the physical principle of conserving energy and damping in harmonic oscillators. This physics-based approach allows smoother convergence throughout the optimization process and wider tunability options. We evaluated our method on a standard set of test functions and demonstrated that, in most cases, it outperforms its natural competitors, including the original PSO, as well as commonly used optimization methods such as COBYLA and Differential Evolution.
Copyright: © 2025 Chernyak et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



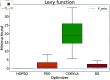
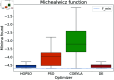



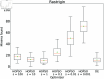
Similar articles
-
Signs and symptoms to determine if a patient presenting in primary care or hospital outpatient settings has COVID-19.Cochrane Database Syst Rev. 2022 May 20;5(5):CD013665. doi: 10.1002/14651858.CD013665.pub3. Cochrane Database Syst Rev. 2022. PMID: 35593186 Free PMC article.
-
Cost-effectiveness of using prognostic information to select women with breast cancer for adjuvant systemic therapy.Health Technol Assess. 2006 Sep;10(34):iii-iv, ix-xi, 1-204. doi: 10.3310/hta10340. Health Technol Assess. 2006. PMID: 16959170
-
Factors that impact on the use of mechanical ventilation weaning protocols in critically ill adults and children: a qualitative evidence-synthesis.Cochrane Database Syst Rev. 2016 Oct 4;10(10):CD011812. doi: 10.1002/14651858.CD011812.pub2. Cochrane Database Syst Rev. 2016. PMID: 27699783 Free PMC article.
-
Antidepressants for pain management in adults with chronic pain: a network meta-analysis.Health Technol Assess. 2024 Oct;28(62):1-155. doi: 10.3310/MKRT2948. Health Technol Assess. 2024. PMID: 39367772 Free PMC article.
-
Transfusion thresholds for guiding red blood cell transfusion.Cochrane Database Syst Rev. 2021 Dec 21;12(12):CD002042. doi: 10.1002/14651858.CD002042.pub5. Cochrane Database Syst Rev. 2021. PMID: 34932836 Free PMC article.
References
-
- Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Computat. 1997;1(1):67–82. doi: 10.1109/4235.585893 - DOI
-
- Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95 - International Conference on Neural Networks. vol. 4; 1995. p. 1942–8. Available from: https://ieeexplore.ieee.org/document/488968
-
- Holland JH. Genetic Algorithms. Scientific American. 1992;267(1):66–73.
-
- Storn R, Price K. Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J Global Optim. 1997;11(4):341–359. doi: 10.1023/a:1008202821328 - DOI
LinkOut - more resources
Full Text Sources

