Harmonic oscillator based particle swarm optimization

Abstract

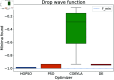
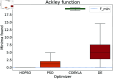
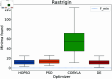
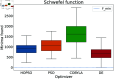
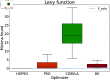
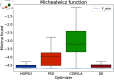
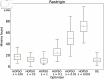
Numerical optimization techniques are widely applied across various fields of science and technology, ranging from determining the minimal energy of systems in physics and chemistry to identifying optimal routes in logistics or strategies for high-speed trading. Here, we present a novel method that integrates particle swarm optimization (PSO), a highly effective and widely used algorithm inspired by the collective behavior of bird flocks searching for food, with the physical principle of conserving energy and damping in harmonic oscillators. This physics-based approach allows smoother convergence throughout the optimization process and wider tunability options. We evaluated our method on a standard set of test functions and demonstrated that, in most cases, it outperforms its natural competitors, including the original PSO, as well as commonly used optimization methods such as COBYLA and Differential Evolution.

Fig 1. An example of the movement of a particle in a two-dimensional space based on the PSO algorithm in a single iteration.

An inertia term given by velocity that drives the particle in some direction (violet arrow), a memory term (p_j) that influences the particle’s trajectory based on its best known position (green arrow), and a global-best cooperation term (g) that reflects the best result amongst the entire swarm (red) constitute the particle’s projected movement (yellow arrow). The i indicates iteration, while j indicates particle number.

Fig 2. The effect of randomness in the singular values of the dynamic matrix M, with c1=c2=2.05 and for χ=0.729.

For large r, the difference between the singular values is large, increasing the probability of velocity explosions or death.

Fig 3. Visualization of HOPSO in one-dimension.

In one-dimension, the particle j oscillates about the attractor a_j which is set half-way between its personal best (p_j) and the swarm’s global best (g) based on the weighted average equation (16). The damping is switched off when the amplitude decreases, in the depicted case to approximately twice (m = 2.05) the distance between the attractor and one of the best positions.

Fig 4. Performance of the optimizers on cross-in-tray function.

Except for COBYLA, all other optimizers converge to the minima, with HOPSO and PSO performing much better than their competitors.

Fig 5. Performance of the optimizers on Beale function.

All optimizers except for COBYLA converge reasonably well, with PSO and COBYLA failing to reach the precision of HOPSO and DE. DE performs more precisely than HOPSO but fails to consistently optimize the function successfully. This can be seen in Table 3, where for Beale, DE has a higher mean value.

Fig 6. Performance of the optimizers on Goldstein-Price function.

Here COBYLA performs poorly compared to its competitors, which solve the problem adequately. In terms of accuracy, HOPSO outperforms the other optimization methods.

Fig 7. Performance of the optimizers on Drop-Wave function.

Unlike in previous cases, none of the optimizers converges perfectly within a given budget. Here, both PSO and HOPSO do reach better results than COBYLA and DE, with HOPSO achieving higher accuracy.

Fig 8. Performance of the optimizers on Ackley function.

All optimizers except HOPSO fail to converge to the minima, with HOPSO being more precise and more accurate than its competitors.

Fig 9. Performance of the optimizers on Rastrigin function.

All optimizers fail to converge to the minima. However, DE performs the best slightly ahead of HOPSO and PSO which in turn are significantly better than COBYLA.

Fig 10. Performance of the optimizers on Schwefel function.

All optimizers fail to converge to the minima by a significant amount. Among these, DE performs the best, followed by HOPSO and PSO.

Fig 11. Performance of the optimizers on Griewank function.

HOPSO and PSO perform better than the other two competitors by being more precise and accurate. As can be seen from the figure, HOPSO is more precise and has a lower median than PSO.

Fig 12. Performance of the optimizers on Levy function.

Except for HOPSO, all optimizers fail to converge to the minima. HOPSO performs the best followed by PSO, DE and COBYLA.

Fig 13. Performance of the optimizers on Michalewicz function.

HOPSO and DE show the most consistent performance with minimal spread. DE performs the best, slightly ahead of HOPSO, which significantly outperforms both PSO and COBYLA.

Fig 14. Performance of the optimizers on sphere function.

All optimizers converge to the minima. For higher accurate scenarios, HOPSO and PSO perform the best.

Fig 15. Performance of the optimizers on Rosenbrock function.

None of the optimizers successfully converge to the minima. However, DE and COBYLA outperform both PSO and HOPSO, with PSO showing the weakest performance by far.

Fig 16. Performance of the HOPSO optimizer on varying the scaling parameter s on Michalewicz function.

The results of HOPSO with scaling factor set to 0.1 and 1 outperform the previously best-performing optimizer, DE.

Fig 17. Performance of the HOPSO optimizer on varying the scaling parameter s on Rastrigin function.

The results of HOPSO with the setting of the scaling factor s to 1 outperforms the previously best-performing optimizer, DE.