Quadruple-refocused spin-locking: A robust method for high-amplitude T1ρ imaging

Abstract

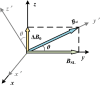
Purpose: Longitudinal relaxation time in the rotating frame (T_1ρ) is a source of tissue-specific contrasts, with applications in detecting myocardial fibrosis, liver fibrosis, and early-stage osteoarthritis. However, T_1ρ measurements are sensitive to static (B₀) and radiofrequency (B₁) magnetic field inhomogeneities. Improving the accuracy of T_1ρ quantification can enable earlier and more reliable detection of pathological changes, providing a basis for early intervention. Therefore, we have developed an improved, quadruple-refocused spin-locking (QR-SL) technique based on existing preparation schemes to obtain a more robust compensation for B₀ and B₁ field inhomogeneities.

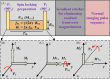
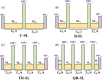
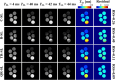
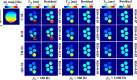
Methods: The QR-SL module consists of four 180° refocusing pulses with opposite phases and five spin-locking (SL) pulses with phase cycling according to the rotary-echo principle. The performance of the proposed QR-SL module is evaluated through numerical simulations and experimental validation in comparison to composite-SL (C-SL), balanced-SL (B-SL), and triple-refocused-SL (TR-SL) preparation modules.

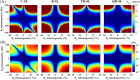
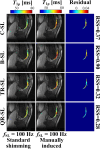
Results: Numerical simulations indicate that the QR-SL module demonstrates improved tolerance to a range of B₀ and B₁ field inhomogeneities compared to the other three modules. In scenarios involving inhomogeneities of both fields, the experimental results show that the residual sum of squares of the QR-SL module was decreased by 24.3%, 68.9%, and 12.5% for in vivo knee cartilage, respectively, compared to the composite SL, balanced SL, and triple-refocused SL preparation modules.

Conclusion: The QR-SL module has the potential to produce more accurate T_1ρ maps, while minimizing artifacts. Consequently, the QR-SL module is more favorable for T_1ρ quantification, especially for low-field and ultralow-field quantitative MRI.

Keywords: T1ρ relaxation; artifacts compensation; field inhomogeneity; quantitative MRI; spin locking.

FIGURE 1

(A) Schematic representation of the typical spin‐locking (SL) module. (B) The initial 90° radio frequency pulse (P₁) is applied along the x‐axis (rotating reference frame) to rotate the longitudinal magnetization, M ₀, into the transverse plane. (C) A spin‐locking pulse (P_SL) along the y‐axis with a duration of T _SL is applied, rotating the magnetization by the total angle, Θ _y , with the frequency, f _SL. The symbol γ denotes the gyromagnetic ratio. (D) The concluding 90° RF pulse (P₂) rotates the magnetization back to its original longitudinal direction.

FIGURE 2

Effective spin‐locking (SL) strength and orientation changes in the rotating frame caused by the B₀ field inhomogeneity. The x‐, y‐, and z‐axes denote the rotating frame of reference. B _e , effective magnetic field; B _SL , field strength of an SL pulse; ΔB ₀ , reduced static field; θ, tilt angle.

FIGURE 3

Schematic representations of the spin‐locking (SL) preparation modules explored in this study: composite‐SL (C‐SL ¹⁶ ) (A); balanced‐SL (B‐SL ¹⁸ ) (B); triple‐refocused‐SL (TR‐SL ¹⁹ ) (C); and our proposed quadruple‐refocused‐SL (QR‐SL) (D). The QR‐SL module consists of five SL pulses with phase cycling according to the rotary‐echo principle and four 180° refocusing pulses with opposite phases (+y/+y/−y/−y).

FIGURE 4

Numerical simulation results. The calculated M _z trajectories (black line) of the composite‐SL (C‐SL) (A), the balanced‐SL (B‐SL) (D), the triple‐refocused‐SL (TR‐SL) (G), and the quadruple‐refocused‐SL (QR‐SL) (J) modules are presented for f _SL = 500 Hz and field imperfections ∆B₀ = 350 Hz and ∆B₁ = −25%. The red line shows the mono‐exponential reference trajectory. The blue dashed line indicates the mono‐exponential fit of the calculated M _z trajectory. The pink area highlights the quantitative error region. The fitting deviations (ΔQ) of T_1ρ and M _z are shown for the C‐SL (B,C), the B‐SL (E,F), the TR‐SL (H,I) and the QR‐SL (J,L) modules.

FIGURE 5

Numerical Bloch simulation comparison of four spin‐locking (SL) modules with f _SL = 500 Hz and T_1ρ: T_2ρ = 1, and field imperfections ∆B₀ = ±600 Hz and ∆B₁ = ±50%. (A,B) The T_1ρ quantification error ∆Q (A) and the residual sum of squares (RSS) (B) were calculated across the ranges of B₀ and B₁ field inhomogeneities with 100 × 100 steps. B‐SL, balanced‐SL; C‐SL, composite‐SL; QR‐SL, quadruple‐refocused‐SL; RSS, residual sum of squares; TR‐SL, triple‐refocused‐SL.

FIGURE 6

(A,B) The proportions that satisfy the criterion ∆Q < 1% are shown for various f _SL points with T_1ρ: T_2ρ = 1 (A) and various T_1ρ: T_2ρ ratios with f _SL = 500 Hz (B). (C,D) The proportions meeting the residual sum of squares (RSS) < 0.01 criterion are presented for various f _SL points with T_1ρ: T_2ρ = 1 (C) and various T_1ρ: T_2ρ ratios with f _SL = 500 Hz (D). B‐SL, balanced‐SL; C‐SL, composite‐SL; QR‐SL, quadruple‐refocused‐SL; RSS, residual sum of squares; TR‐SL, triple‐refocused‐SL.

FIGURE 7

Experimental results based on the agarose gel phantoms. Various T_1ρ‐weighted images (T _SL = 4, 40, 42, and 44 ms) for each spin‐locking (SL) module are shown, along with the corresponding T_1ρ, residual maps, and residual sum of squares (RSS) in the case of f _SL = 100 Hz and B₁ field deviation = −20%. The results show the performance of the modules without additional gradient‐induced B₀ field deviations. B‐SL, balanced‐SL; C‐SL, composite‐SL; QR‐SL, quadruple‐refocused‐SL; TR‐SL, triple‐refocused‐SL.

FIGURE 8

Experimental results based on the agarose gel phantoms for gradient‐induced B₀ field deviations. For each spin‐locking (SL) module, the corresponding T_1ρ, residual maps, and residual sum of squares (RSS) are presented for f _SL = 100, 500, and 1000 Hz, with B₁ field deviation = −20%, and local field of view varying B₀ = −58…58 Hz (Δf ₀ map induced by the gradient obtained from a liquid phantom). As f _SL increases, the performance of each module is significantly enhanced.

FIGURE 9

Experimental results based on the knee cartilage for gradient‐induced B₀‐field deviations. For each spin‐locking (SL) module, the T_1ρ under standard shimming, T_1ρ under manually induced field imperfections (when f _SL = 100 Hz, B₁ field deviation = −20% and local field of view varying B₀ = −77…77 Hz), residual maps, and residual sum of squares (RSS) are shown. The RSS of the quadruple‐refocused‐SL (QR‐SL) module is decreased by 24.3%, 68.9%, and 12.5%, respectively, compared with the composite‐SL (C‐SL), balanced‐SL (B‐SL), and triple‐refocused‐SL (TR‐SL) modules.

FIGURE 10

Comparison of root mean square (RMS) radiofrequency integrals for the four T_1ρ preparation modules for phantom measurements with f _SL = 100, 500 and 1000 Hz, and T _SL = 4, 38, 40, 42, and 44 ms. The RMS integrals of the quadruple‐refocused‐SL (QR‐SL) module show a relative increase of 13.4%, 2.6%, and 0.7% compared with those of the composite‐SL (C‐SL) module when f _SL = 100, 500, and 1000 Hz and T _SL = 44 ms, respectively.