Pattern Formation as a Resilience Mechanism in Cancer Immunotherapy

Abstract

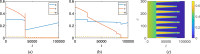
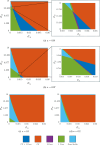
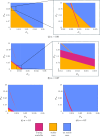
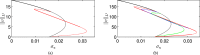
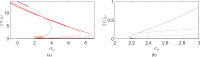
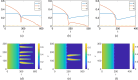
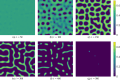
Mathematical and computational modelling in oncology has played an increasingly important role in not only understanding the impact of various approaches to treatment on tumour growth, but in optimizing dosing regimens and aiding the development of treatment strategies. However, as with all modelling, only an approximation is made in the description of the biological and physical system. Here we show that tissue-scale spatial structure can have a profound impact on the resilience of tumours to immunotherapy using a classical model incorporating IL-2 compounds and effector cells as treatment parameters. Using linear stability analysis, numerical continuation, and direct simulations, we show that diffusing cancer cell populations can undergo pattern-forming (Turing) instabilities, leading to spatially-structured states that persist far into treatment regimes where the corresponding spatially homogeneous systems would uniformly predict a cancer-free state. These spatially-patterned states persist in a wide range of parameters, as well as under time-dependent treatment regimes. Incorporating treatment via domain boundaries can increase this resistance to treatment in the interior of the domain, further highlighting the importance of spatial modelling when designing treatment protocols informed by mathematical models. Counter-intuitively, this mechanism shows that increased effector cell mobility can increase the resilience of tumours to treatment. We conclude by discussing practical and theoretical considerations for understanding this kind of spatial resilience in other models of cancer treatment, in particular those incorporating more realistic spatial transport. This paper belongs to the special collection: Problems, Progress and Perspectives in Mathematical and Computational Biology.

Keywords: Immunotherapy; Pattern Formation; Resilience; Solid Tumours.

Fig. 1

(a): Simulations of the ODE model given by Equations (15)-(17); the variables u and w correspond to immunotherapy-related quantities whereas v represents the density of cancer cells. (b): Spatial averages from simulations of the PDE model given by Equations (11)-(13) with homogeneous Neumann boundary conditions. (c): Kymographs of v from the spatial (PDE) simulations in (b). Parameters are given in Table 1 with $\alpha =0.07$, ${\delta }_u={\delta }_w=100$, where ${\sigma }_w=0.5$, and ${\sigma }_u=0.01+0.03\frac{t}{T}$, with the final simulation time given by $T={10}^5$ in all cases

Fig. 2

Classification of the number and type of linearly stable steady states of Equations (15)-(17) for varying ${\sigma }_u$, ${\sigma }_v$ and $\alpha$. Here, ‘CF’ stands for cancer-free equilibrium, and ‘coex’ for coexistence equilibria

Fig. 3

Classification of parameters where Turing instabilities are possible computed via (33) for Equations (11)-(13) across varying ${\sigma }_u$, ${\sigma }_v$ and $\alpha$. All parameters are given in Table 1 with ${\delta }_u=100$ and ${\delta }_w=100$

Fig. 4

Bifurcation diagram for model (11)–(13) showing steady-state values of ${\Vert v\Vert }_{L^1}$ for the same parameter values as in the simulation shown in Fig 1(b)-(c) except treating ${\sigma }_u$ as a constant bifurcation parameter. Panel (a) is on a domain of size $L=30$, and panel (b) is on a domain of size $L=300$. Thick solid curves are linearly stable steady states, and dotted curves are unstable. The black curve corresponds to a homogeneous equilibrium (i.e. a steady state of (15)–(17)), whereas the coloured curves represent patterned solution branches

Fig. 5

Bifurcation diagram for model (11)–(13) showing steady state values of ${\Vert v\Vert }_{L^1}$ for the same parameter values as in the simulation shown in Fig 1(e)-(f) except treating ${\sigma }_w$ as a constant bifurcation parameter and using a domain of size $L=30$. Panel (b) is a zoomed version showing the complexity of branches near the cancer-free equilibrium for ${\sigma }_w\in [2,3]$ (the red boxed region in panel (a)). Thick solid curves are linearly stable steady states, and dotted curves are unstable. The black curves correspond to homogeneous equilibria (i.e. steady states of (15)–(17)), whereas the red curves represent patterned solution branches

Fig. 6

Simulations of the ODE (panel (a)) and PDE (panels (b)-(c)) models as in Figure 1 with ${\sigma }_u=0.014$, and ${\sigma }_w=10\frac{t}{T}$, with the final simulation time given by $T={10}^5$ in all cases

Fig. 7

Simulations of the PDE model (11)-(13) as in Figure 1 with a different final simulation time of $T=600$ in (a), (d), $T=500$ in (b), (e), and $T=400$ in (c), (f). Spatial averages are given in (a)-(c), whereas kymographs of v are shown in (d)-(f). Recall that the varying treatment parameter is given as ${\sigma }_u=0.01+0.03t/T$, so that the treatment rate increases along each row

Fig. 8

Simulations of the ODE (panel (a)) and PDE (panels (b)-(c)) models as in Figure 1 with ${\sigma }_u=0.014$ and ${\sigma }_w=18(\frac{t}{T}H\left(0.5,-,\frac{t}{T}\right)+(1-(\frac{t}{T}))H\left(\frac{t}{T},-,0.5\right))$, where H denotes the heaviside step-function

Fig. 9

Snapshots from simulations of Equations (11)-(13) in a square domain of side length $L=300$ with homogeneous Neumann boundary conditions, ${\sigma }_u=0.015+5\times {10}^{-5}t$, ${\sigma }_w=0.5$, $\alpha =0.07$, ${\delta }_u={\delta }_w=100$, and all other parameters as in Table 1. The cancer cell density v is plotted, with u and w exhibiting in-phase patterned solutions in each panel

Fig. 10

Snapshots from simulations of Equations (11)-(13) in a circular domain of diameter $L=300$ with homogeneous Neumann boundary conditions, ${\sigma }_u=0.014$, ${\sigma }_w=20\left(\frac{t}{400},H,\left(0.5,-,\frac{t}{400}\right),+,\left(1,-,\frac{t}{400}\right),H,\left(\frac{t}{400},-,0.5\right)\right)H\left(1,-,\frac{t}{400}\right)$, $\alpha =0.07$, ${\delta }_u={\delta }_w=100$, and all other parameters as in Table 1. The cancer cell density v is plotted, with u and w exhibiting in-phase patterned solutions in each panel

Fig. 11

Snapshots from simulations of Equations (11)-(13) in a square domain of side length $L=300$, ${\sigma }_u=0.007$, ${\sigma }_w=0$, $\alpha =0.1$, ${\delta }_u=100$, ${\delta }_w=1000$, and all other parameters as in Table 1. The boundary conditions for u and v are homogeneous Neumann, whereas we implement Equation (35) for w on the four boundaries with $B_w(t)=0.01t$. The cancer cell density v is plotted, with u and w exhibiting in-phase patterned solutions in each panel

Fig. 12

Snapshots from simulations exactly as in Figure 11 except with ${\delta }_u=10$

Fig. 13

Snapshots from simulations exactly as in Figure 11 except with ${\delta }_u=1000$

Fig. 14

Snapshots from simulations of Equations (11), (13), and (36) in a circular domain of diameter $L=100$ with homogeneous Neumann boundary conditions, ${\sigma }_u=0.015+5\times {10}^{-5}t$, ${\sigma }_w=0.5$, $\alpha =0.07$, ${\delta }_u={\delta }_w=5$, and all other parameters as in Table 1. The cancer cell density v is plotted, with u and w exhibiting in-phase patterned solutions in each panel